|
 =p/z
=p/z  y
y  x
x  p
p  z
z  y
y  z
z  x,
x,
 =y
=y  z
z 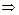 p
p  x
x  y/z
y/z  p
p  x
x  y,
y,
 =z/x
=z/x 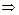 (y
(y  p
p  (x
(x  y
y  z))
z))  x
x  p,
p,
 =x
=x  y
y  z
z  p
p  x
x  y
y  x/z
x/z 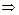 y
y  p,
p,
 =x/z
=x/z  p
p  x
x  p
p  x
x  z
z  p
p  y,
y,
 =x
=x  z
z 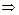 y
y  p
p  x
x  y
y  z
z  p/x
p/x  z,
z,
 =y/p
=y/p  x
x  y
y  p
p  z
z  x
x  z
z  x,
x,
 =p
=p  y
y  x
x  z
z  p
p  y/z
y/z  x
x  p,
p,
 =p
=p 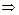 z
z  (y
(y  x
x  z)
z)  p/x
p/x  z
z  y
y  x,
x,
 =x
=x  y
y  z
z  x
x 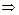 (y
(y  z)
z)  y
y  p/x,
p/x,
 =z/x
=z/x  p
p  y
y  x
x  y
y 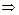 z
z  x
x  p,
p,
 =y
=y  x
x  z
z  p
p  y
y  x
x  y
y  z/x,
z/x,
 =z
=z  y
y  x/y
x/y  z
z  x
x  y
y 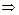 z
z  p,
p,
 =x
=x  y
y 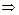 z
z  x
x  p
p  y/z
y/z  x
x  y,
y,
 =x
=x 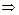 y
y  z
z  p
p  x
x  y/x
y/x  z
z  y,
y,
 =p
=p  x
x  y/z
y/z  p
p  y
y  x
x  z
z 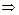 y
y  p,
p,
 =x
=x  z
z  p/z
p/z  x
x  y
y  z
z  p
p  p
p  y,
y,
 =z
=z  p
p  x
x  p
p  y
y  x/z
x/z  y
y  z,
z,
 =x
=x  y
y  z
z  x/y
x/y  z
z  p
p  z
z  x,
x,
 =x
=x  y
y  p/y
p/y  z
z  y
y  z
z  p
p  x,
x,
 =z
=z  p
p  z/y
z/y  x/z
x/z  p
p  y
y  x,
x,
 =p
=p  y
y  z
z  p
p  y/x
y/x  y
y  p
p  y,
y,
 =p/y
=p/y  z
z  p
p  x
x  z
z  y
y  x
x  z
z  y,
y,
 =z
=z  p/x
p/x  z
z  y
y  p
p  y
y 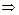 x
x  z,
z,
 =y
=y  x/z
x/z  p
p  x
x  y
y  z
z  x
x  p,
p,
 =p
=p  x
x  z/p
z/p  x
x  y
y  z
z  p
p  y,
y,
 =p
=p  z
z  x
x  y
y  y/p
y/p  z
z  x
x  p,
p,
 =x
=x  y
y  z
z  p
p  z
z  x/y
x/y  p
p 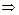 z,
z,
|
 =z
=z  y
y  p
p  z
z  y
y  p/x
p/x  y
y  z,
z,
 .
.
 Аналогично для булевой функции
Аналогично для булевой функции  получаем её представление в виде совершенной КНФ:
получаем её представление в виде совершенной КНФ:

Приведенные теоремы позволяют сформулировать следующую теорему:
Теорема 6 (о функциональной полноте). Для любой булевой функции  найдется формула
найдется формула  , представляющая функцию
, представляющая функцию  .
.
 Если
Если 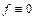 , то существует представляющая ее формула
, то существует представляющая ее формула  , находящаяся в СДНФ:
, находящаяся в СДНФ:

 и такое представление единственно с точностью до порядка следования конституент единицы. Если
и такое представление единственно с точностью до порядка следования конституент единицы. Если  , то существует представляющая ее формула
, то существует представляющая ее формула  , находящаяся в СКНФ:
, находящаяся в СКНФ:

и такое представление единственно с точностью до порядка следования конституент нуля.
Указанная теорема дает возможность сформулировать алгоритм перехода от табличного задания функции  к ее представлению в виде СДНФ(СКНФ).
к ее представлению в виде СДНФ(СКНФ).
 2020-07-12
2020-07-12 106
106








