1. Исходную формулу заданной функции приводим с помощью эквивалентных преобразований к ДНФ.
2. Конъюнкты ДНФ преобразовываем в конституенты единицы по следующим правилам:
а) если в конъюнкт входит некоторая переменная вместе со своим отрицанием, то этот конъюнкт удаляется из ДНФ;
б) если в конъюнкт одна и та же литера  входит несколько раз, то удаляются все литеры
входит несколько раз, то удаляются все литеры  , кроме одной;
, кроме одной;
в) если в некоторый конъюнкт  не входит переменная
не входит переменная  , то этот конъюнкт заменяется на эквивалентную формулу
, то этот конъюнкт заменяется на эквивалентную формулу 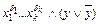 и, применяя закон дистрибутивности, приводим полученную формулу к ДНФ; если недостающих переменных несколько, то для каждой из них к конъюнкту добавляем соответствующую формулу вида
и, применяя закон дистрибутивности, приводим полученную формулу к ДНФ; если недостающих переменных несколько, то для каждой из них к конъюнкту добавляем соответствующую формулу вида  ;
;
г) если в полученной ДНФ имеется несколько одинаковых конституент единиц, то оставляем только одну из них. В результате получается ДНФ.
Пример 1-10. Найти СДНФ для ДНФ  .
.
Имеем 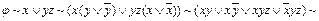

 .
.
Описание алгоритма привидения КНФ к СКНФ аналогично вышеизложенному описанию алгоритма приведения ДНФ к СДНФ.
Совершенно полиноминальная нормальная форма (СПНФ).
Существует еще и третья форма представления ФАЛ – совершенная поли номинальная нормальная форма (СПНФ).
Алгоритм построения СПНФ.
1. Исходную ФАЛ  представить в СДНФ.
представить в СДНФ.
2. В конституентах единицы СДНФ произвести замену  .
.
3 Знак  между конституентами единицы в СДНФ заменить на знак
между конституентами единицы в СДНФ заменить на знак  .
.
4. Окончательно упростить выражение для  в СПНФ путем раскрытия скобок, сокращения одинаковых слагаемых при использовании эквивалентностей:
в СПНФ путем раскрытия скобок, сокращения одинаковых слагаемых при использовании эквивалентностей: 
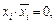

 .
.
|
 2020-07-12
2020-07-12 274
274








