Алгоритм приведения формулы к ДНФ

1. Выражаем все логические операции, участвующие в построении формулы, через { 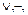&}, используя вышеприведенные эквивалентности.

2. Используя законы де Моргана, переносим все отрицания к переменным и сокращаем двойные отрицания по правилу: .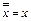

3. Используя закон дистрибутивности 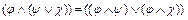, преобразуем формулу так, чтобы все конъюнкции выполнялись раньше дизъюнкций.

Пример 1-6. Привести к ДНФ формулу .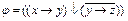

.

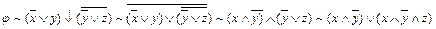Приведение формул к КНФ производиться аналогично приведению её к ДНФ, только вместо п. 3. применяется пункт:

: 3’. Используя закон дистрибутивности: 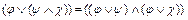 преобразует формулу так, чтобы все дизъюнкции выполнялись, раньше конъюнкции.

Пример 1-7. Приведем к КНФ формулу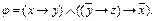

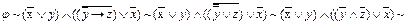
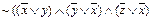, являющейся КНФ.