Глава 2. Задания к практическим занятиям, выполнению расчетно-графических работ и для самостоятельной работы по функциям алгебры логики

 

2.1 ЗАДАЧИ И УПРАЖНЕНИЯ I^ГО – ТИПА *.

 

1. Доказать, что число всех булевых функций от n аргументов равно .

2. Записать в совершенных ДНФ и КНФ булеву функцию , принимающую значение 1 на наборах с номерами 3,4, 7.

3. Записать в ДНФ и КНФ булеву функцию , принимающую значение 0 на наборах с номерами 2, 6, 7, 8, 11, 12.

4. Проверить справедливость равенства .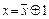

5. Проверить справедливость следующих равенств:

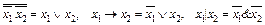
6. Показать, что число булевых функций, существенно зависящих от п аргументов, определяется рекуррентным соотношением

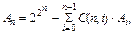
где  — число булевых функций, зависящих от  аргументов.

7. Булева функция , зависящая от трех аргументов, называется мажоритарной, если имеет место равенство  Будем обозначать эту операцию знаком # и записывать  

Доказать, что имеют место следующие соотношения:

1)

2)

3)

8. Найти минимальную ДНФ функции , принимающей значение 1 на наборах 0, 1, 2, 5, 6, 7, 8, 12, 13.

9. Найти минимальную ДНФ функции , принимающей значение 1 на наборах с номерами от  0 до 7, от 11 до 21 и от 26 до 31.

10. Функция  равна 1 на наборах 1, 3, 4 и не определена на наборе с номером 5. Найти ее минимальную ДНФ.

 

между всеми компонентами наборов и установлено соотношение , = . Отметим что при таком определении набор <1, 0, 1, 1> не меньше набора <1, 0, 1, 0>, а наборы <1, 0, 1, 1> и <0, 1, 1, 1> несравнимы.

 

Определение 6. Функция  называется монотонной, если для любых двух наборов  и , таких, что , имеет место равенство:

4. M – класс монотонных функции. В таблице 1 класс

Число функций этого класса M оценивается асимптотически:

,

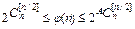где  - число монотонных ФАЛ зависящих от n аргументов, а   A - некоторая константа.

Определение 7. Функция называется симметричной, если она не изменяется при произвольной перенумерации аргументов:

= ,                    

где  - любая перестановка аргументов .

Определение 8. Функция  называется линейной, если она представима в следующем виде:

,               (1 – 23)

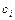
где коэффициенты , 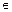{0,1}, = .

5. L – класс линейных функции.

Число членов этого класса равно . В таблице 1 класс . Например, .

 

Методы определения линейности ФАЛ.