Коэффициенты 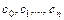 из формулы (1 – 23) линейной функции определяются из соотношений:
из формулы (1 – 23) линейной функции определяются из соотношений:
 (1 – 24)
(1 – 24)
|
|
системы функций Ф необходимо и достаточно, чтобы для всякого предполного класса в Ф нашлась функция, в него не входящая.
Оказывается, что все предполные классы легко перечисляются. Ими являются классы 
Удобнее доказывать не предполноту этих классов, а непосредственно критерий полноты, который получается из этого факта и задачи 11. Напротив, исходя из критерия полноты, докажем предполноту классов  и то, что всякий собственный функционально замкнутый класс содержится в одном из них.
и то, что всякий собственный функционально замкнутый класс содержится в одном из них.
Вначале докажем одно вспомогательное утверждение:
12. Доказать, что отождествлением переменных из всякой функции, не сохраняющей нуль (единицу), можно получить функцию от одной переменной, обладающую этим же свойством, т. е. 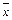 или 1 (соответственно
или 1 (соответственно  или 0).
или 0).
Сформулируем критерий полноты ФАЛ.
Теорема 8(Пост). Для полноты системы функций  необходимо и достаточно, чтобы для каждого из классов
необходимо и достаточно, чтобы для каждого из классов  в Ф нашлась функция
в Ф нашлась функция  , ему не принадлежащая.
, ему не принадлежащая.
13. Доказать теорему Поста для системы  .
.
При проверке, выполняются ли для некоторой системы функций  условия теоремы Поста, будем составлять таблицы, которые назовем таблицами Поста. Они будут иметь вид:
условия теоремы Поста, будем составлять таблицы, которые назовем таблицами Поста. Они будут иметь вид:

| 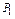
| 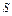
| 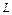
| 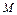
| |

| — | ||||

| — | + | |||
| … | … | … | … | … | … |

| — | — | + | ||

| — | — |
В клетках таблицы Поста ставится плюс или минус, в зависимости от того, входит функция, стоящая в данной строке, в класс, стоящий в данном столбце, или не входит. Для полноты системы функций необходимо и достаточно (в силу теоремы Поста), чтобы в каждом столбце стоял хотя бы один минус.
14. Решить задачу 2, используя теорему Поста.
15. Исходя из теоремы Поста, сформулировать критерий неполноты системы функций.
|
|



Заданная функция является нелинейной, т.к. полином Жегалкина для заданной функции нелинейный.
Пример 1-14. а) 


Исходная функция нелинейная.
б) 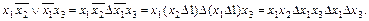
Исходная функция нелинейная.
в) 
Исходная функция линейная.
При получении полинома Жегалкина из СДНФ исходной ФАЛ можно сразу заменять операцию 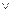 на операцию
на операцию  , т.к. в эквивалентности (1-17):
, т.к. в эквивалентности (1-17):  формулы
формулы  и
и  являются различными конституентами единицы, их произведение
являются различными конституентами единицы, их произведение  и тогда
и тогда 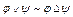 .
.
Замечательное свойство классов ФАЛ (классов Поста):
Каждый класс Поста замкнут относительно операций замены переменных и суперпозиций, т.е. с помощью этих операций из функций, принадлежащих данному классу, можно получить только функции из этого же класса.
1.9 Функционально замкнутые классы. Критерий полноты *.
Среди рассмотренных нами вопросов одними из наиболее важных были вопросы о представимости функций алгебры логики в том или ином виде (ДНФ, КНФ, полиномы Жегалкина). Всякий раз фактически речь шла о возможности представить функции алгебры логики в виде суперпозиций некоторого фиксированного множества функций. Общая проблема ставится следующим образом:
Имеется некоторая система  функций алгебры логики
функций алгебры логики  . Для всякой ли функции алгебры логики существует равносильная ей суперпозиция функций из системы
. Для всякой ли функции алгебры логики существует равносильная ей суперпозиция функций из системы  ?
?
Определение 9. Система функций  называется полной, если всякая функция алгебры логики представима посредством суперпозиций функций из системы Ф.
называется полной, если всякая функция алгебры логики представима посредством суперпозиций функций из системы Ф.
Из представимости функций в виде СДНФ следует полнота системы функций  . Случай тождественного нуля не приводит к ограничениям, поскольку
. Случай тождественного нуля не приводит к ограничениям, поскольку  .
.
Предлагаемые далее задачи нумеруются: 1÷27.
1. С полнотой какой системы функций связана представимость функций полиномами Жегалкина?
2. Доказать полноту следующих систем функций:
а) 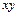 ,
,  ; б)
; б) 
 ; в)
; в) 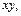
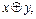 1; г)
1; г) 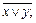 д)
д)  и)
и) 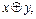
 1;
1;
ж) 
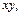 0, 1; з)
0, 1; з) 
 ; е)
; е)  0.
0.
3. Доказать, что если некоторая система функций  полна, то и система двойственных функций
полна, то и система двойственных функций 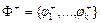 полна.
полна.
4. Показать, что ниже следующие системы функций не являются полными: а)  1; б)
1; б) 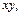
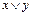 ; в)
; в) 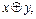
 г)
г) 
 ; д)
; д)  0, 1.
0, 1.
Анализ решения задачи 4 выявляет следующую идею доказательства неполноты системы функций Ф. Нужно найти какое-либо свойство, которое сохраняется при суперпозиции («наследственное» свойство) и которым обладают все функции системы Ф, хотя не все функции алгебры логики им обладают. Действительно, тогда функцию, не обладающую этим наследственным свойством, нельзя представить в виде суперпозиции функций из Ф. При исследовании наследственных свойств функций удобно пользоваться понятием функционально замкнутого класса.
Определение 10. Всякая совокупность  функций алгебры логики, замкнутая относительно суперпозиции (т. е. такая, что суперпозиция функций из
функций алгебры логики, замкнутая относительно суперпозиции (т. е. такая, что суперпозиция функций из  снова принадлежит
снова принадлежит  ), называется функционально замкнутым классом.
), называется функционально замкнутым классом.
Очевидно, что совокупность функций, обладающих каким-либо наследственным свойством, является функционально замкнутым классом и, обратно, свойство принадлежать какому-либо функционально замкнутому классу является наследственным. Другими словами, эти понятия сводятся одно к другому.
5. Какие из указанных ниже систем функций являются функционально замкнутыми классами:
а) функции от одной переменной;
б) функции от двух переменных;
|
г) линейные функции;
д) самодвойственные функции;
е) монотонные функции;
ж) монотонно убывающие функции;
з) функции, сохраняющие нуль;
и) функции, сохраняющие единицу;
к) функции, сохраняющие и нуль, и единицу;
л) функции, сохраняющие нуль, но не сохраняющие единицу?
6. 1) Доказать, что пересечение функционально замкнутых классов — функционально замкнутый класс.
2) Доказать, что совокупность функций, двойственных функциям из функционально замкнутого класса, образует функционально замкнутый класс (двойственный класс).
7. Является ли объединение функционально замкнутых классов функционально замкнутым классом?
Определение 11. Функционально замкнутые классы, отличные от пустого класса и от совокупности всех функций алгебры логики, называются собственными функционально замкнутыми классами.
8. Доказать, что дополнение собственного функционально замкнутого класса (совокупность функций, в него не входящих) не может быть функционально замкнутым классом.
Определение 12. Минимальная полная система функций (т. е. такая полная система функций, удаление из которой любой функции делает систему неполной) называется базисом.
9. Показать, что полные системы из задачи 2 являются базисами.
Для полноты системы функций необходимо, чтобы для всякого собственного функционально замкнутого класса в ней нашлась функция, не входящая в этот класс. Это условие является также и достаточным.
10. Доказать, что для полноты системы функций Ф необходимо и достаточно, чтобы для всякого функционально замкнутого класса, не совпадающего с множеством всех функций, в Ф нашлась функция, не принадлежащая этому классу.
Для решения вопроса о полноте нет необходимости в переборе всех классов, так как можно ограничиться максимально функциональными замкнутыми классами.
Определение 13. Собственный функционально замкнутый класс называется предполным, если он не содержится ни в каком функционально замкнутом классе, отличном от самого себя и от класса всех функций алгебры логики.
|
Проверка линейности функции  сводиться к нахождению коэффициентов
сводиться к нахождению коэффициентов 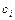 по формулам (1 – 24) и сопоставлению таблиц истинности данной формулы
по формулам (1 – 24) и сопоставлению таблиц истинности данной формулы 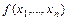 и полученной формулы
и полученной формулы  .
.
Пример 1-12. Установить, является ли линейной функция:
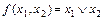 .
.
имеем 
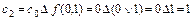 .
.
Таким образом, 
 Сопоставляя таблицы истинности формул
Сопоставляя таблицы истинности формул 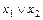 и
и  , убеждаемся, что они не совпадают; следовательно, функция
, убеждаемся, что они не совпадают; следовательно, функция  нелинейная.
нелинейная.
 2020-07-12
2020-07-12 165
165








