Основные классы функций алгебры логики

Для решения ряда принципиальных вопросов, связанных с теорией ФАЛ и с практическим применением результатов этой теории для анализа и синтеза схем, полезно рассмотреть основные классы ФАЛ (классы Поста).

1. 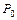 - класс функций, сохраняющих константу нуль, т. е. таких функций, для которых имеет место равенство: .

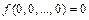В таблице 1 класс 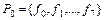. Очевидно, что при фиксированном n число функций этого класса составляет половину всех функций алгебры логики, т. е.  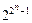функций.

2. 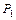- класс функций, сохраняющих константу единица, будет определен как класс функций, для которых имеет место равенство: .

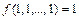В таблице 1 класс 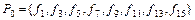. Этот класс также состоит из  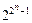функции.

Определение 4.   Функция 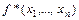называется двойственной к функции 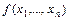, если имеет место равенство.

=

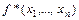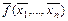
Определение 5. Функция 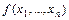 называется самодвойственной, если она совпадает с двойственной себе функцией, т. е. имеет место равенство:

=

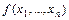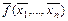
3. 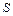 - класс самодвойственных функций. В таблице 1 класс .

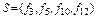Число членов этого класса равно 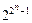, так как самодвойственная функция от n аргументов полностью определяется на половине наборов значений аргументов.

16

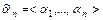Будем говорить, что набор значений аргумента не меньше набора значений аргументов 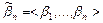, т.е. 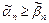, если

11. Разработать тест распознавания противоречивого задания недоопределенной булевой функции 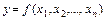 (функция задана противоречиво, если () ()).

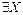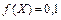12. Найти минимальную ДНФ булевой функции

 

13. Определить скобочную форму булевой функции

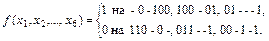
14. Найти мощность единичной области недоопределенной булевой функции 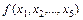после ее доопределения:

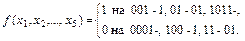
15. Проверить линейность булевой функции

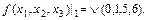
16. Установить, является ли самодвойственной функция эквивалентности.

17. Проверить монотонность конъюнкции от n аргументов.

18. Привести пример монотонной функции, которая одновременно была бы линейной.

19. Привести пример самодвойственной функции, которая одновременно была бы линейной.

20. Привести пример линейной и монотонной функций.

21. Убедиться, что функции Шеффера и Вебба не являются ни линейными, ни монотонными, ни самодвойственными.

22. Установить, образует ли булева функции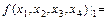

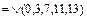 базис в .

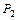2З. Верно ли утверждение: если булева функция существенно зависит более чем от одного аргумента и она монотонна, то она несамодвойственна?

24. Верно ли утверждение: если булева функция существенно зависит более чем от одного аргумента и она линейна, то она немонотонна?

25. Найти все булевы функции, удовлетворяющие системе уравнений

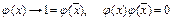
26. Доказать следующую теорему: при суперпозиции линейных функций получаются линейные функции.

25

27. Доказать теорему: при суперпозиции самодвойственных функций вновь получаются самодвойственные функции.