1. Выбрать в таблице задания функции все наборы ( ) аргументов, на которых
) аргументов, на которых  .
.
2. Выписать конституенты единицы  , соответствующие этим наборам аргументов; при этом, если аргумент
, соответствующие этим наборам аргументов; при этом, если аргумент  входит в данный набор как 1, он вписывается без изменений
входит в данный набор как 1, он вписывается без изменений  в конъюнкт
в конъюнкт  ; если же
; если же  входит в данный набор как 0, то в соответствующий конъюнкт вписывается его отрицание (
входит в данный набор как 0, то в соответствующий конъюнкт вписывается его отрицание ( ).
).
3. Все полученные конституенты единицы соединяются знаками дизъюнкции.
Пример 1-9. Найти СДНФ и СКНФ функции  , заданной следующей таблицей истинности:
, заданной следующей таблицей истинности:

| 
| 
| 
| Конституенты: 
|
| 0 | 0 | 0 | 1 | 
|
| 0 | 0 | 1 | 1 | 
|
| 0 | 1 | 0 | 0 | 
|
| 0 | 1 | 1 | 0 | 
|
| 1 | 0 | 0 | 0 | 
|
| 1 | 0 | 1 | 1 | 
|
| 1 | 1 | 0 | 0 | 
|
| 1 | 1 | 1 | 1 | 
|
( ) – наборы аргументов
) – наборы аргументов  .
.


|
|
2.2 ЗАДАЧИ И УПРАЖНЕНИЯ IIГО – ТИПА *.
1. Проверить полноту заданной системы функций. Для функционально полной системы выделить базис.
1) F={  ,
,  }, где
}, где  =x
=x  y,
y,  =x
=x  yz,
yz,
2) F={  ,
,  ,
,  ,
,  }, где
}, где  =xy,
=xy,  =x~yz,
=x~yz,  =0,
=0,  =1,
=1,
3) F={  ,
,  ,
,  ,
,  }, где
}, где  =(x
=(x  y)
y)  (y~z),
(y~z),  =(x/(xy))
=(x/(xy))  z,
z,  =x
=x  y,
y,
 =0,
=0,
4) F={  ,
,  ,
,  }, где
}, где  =(0110 1001),
=(0110 1001),  =(1000 1101),
=(1000 1101),  =(0001 1100)
=(0001 1100)
5) F={  ,
,  ,
,  }, где
}, где  =(0100 0100),
=(0100 0100),  =(1111 1100),
=(1111 1100),  =(1000 0000)
=(1000 0000)
2. Составить все возможные базисы из функций двух переменных.
3. Для заданной функции  :
:
1) построить таблицу истинности;
2) построить изображение на кубе;
З) найти СДНФ и СКНФ;
4. Определить принадлежность классам Поста.
5. Построить функционально полную систему функции так, чтобы эта система была базисом и содержала  .
.
 =x
=x  p/z
p/z  y
y  x
x  p
p  z
z  x
x  y
y  z,
z,
 =p
=p  y
y  y
y  x
x  z
z  p/y
p/y  z
z  x,
x,
 ==p/z
==p/z  x
x  y
y  z
z  y
y  p
p  x
x  y
y  z,
z,
 =y
=y  z
z  p
p  x
x  z
z  p
p  y/y
y/y  z,
z,
 =z
=z  y
y  p
p  x
x  z
z  p/z
p/z  y
y  x,
x,
 =x
=x  y
y  p
p  x
x  z
z  x/y
x/y  z
z  x
x 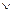 z,
z,
 =z
=z  y
y  x
x  z
z  p
p  x
x  z/y
z/y  p,
p,
 =y
=y  z
z  p
p  x
x  z
z  p
p  y/p
y/p  z,
z,
 =p
=p  x
x  z
z  y
y  p
p  z
z  y/z
y/z  x,
x,
 =x/y
=x/y  z
z  p
p  x
x  y
y  z
z  p
p  y
y  z,
z,
 =z
=z  p
p  y
y  z
z  x
x  p
p  y
y  z/x,
z/x,
 =x/z
=x/z  p
p  y
y  x
x  z
z  p
p  z
z  p,
p,
 =x
=x  y
y  z
z  p
p  x/y
x/y  z
z 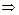 p
p  z,
z,
Пусть ( ) – набор логических переменных,
) – набор логических переменных,  - набор нулей и единиц.
- набор нулей и единиц.
Конституентой единиц набора  называется конъюнкт:
называется конъюнкт:
 .
.
Конституентой нуля набора  называется дизъюнкт:
называется дизъюнкт:
 .
.
Отметим, что  (
( ) тогда и только тогда, когда
) тогда и только тогда, когда  .
.
Совершенной ДНФ называется дизъюнкция некоторых конституент единиц, среди которых нет одинаковых, а совершенной КНФ называется конъюнкция некоторых конституент нуля, среди которых нет одинаковых. Таким образом, СДНФ (СКНФ) есть ДНФ (КНФ), в которой в каждой конъюнкт (дизъюнкт) каждая переменная  из набора (
из набора ( ) входит ровно один раз, причем входит либо сама
) входит ровно один раз, причем входит либо сама  , либо ее отрицание
, либо ее отрицание  .
.
Пример 1-8. Формула  есть конституента единицы
есть конституента единицы  ; формула
; формула  есть конституента нуля
есть конституента нуля  ; формула
; формула  - СДНФ, формула (
- СДНФ, формула ( )
)  - СКНФ.
- СКНФ.
Для решения задачи нахождения СДНФ и СКНФ, эквивалентных исходной формуле  , предварительно рассмотрим разложения булевой функции
, предварительно рассмотрим разложения булевой функции 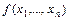 по
по  переменным (для определенности по
переменным (для определенности по  ) –разложения Шеннона.
) –разложения Шеннона.
Теорема 4 (первая теорема Шеннона). Любая булева функция  представима в виде разложения Шеннона:
представима в виде разложения Шеннона:
 .
.
 при
при  для булевой функции
для булевой функции  ,получаем ее представление в виде совершенной ДНФ:
,получаем ее представление в виде совершенной ДНФ:
 .
.
В силу принципа двойственности для булевых алгебр справедлива:
Теорема 5 (вторая теорема Шеннона). Любая булева функция  представима в виде разложения Шеннона:
представима в виде разложения Шеннона:
|
 =y
=y  p
p  x
x  z
z  p
p  y/p
y/p  x
x  z,
z,
 =p
=p  x
x  z
z  y
y  p/z
p/z  y
y 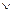 x
x  y,
y,
 =x/p
=x/p  y
y  x
x  p
p  z
z  y
y  z
z  y,
y,
 =p
=p  z
z  x
x  y
y  (z
(z  p
p  x)/y
x)/y 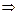 p,
p,
 =z
=z  x
x  y/x
y/x  p
p  x
x  z
z  p
p  x,
x,
 =p
=p  x
x  y
y  z/p
z/p  p
p  x
x  z
z  y,
y,
 =z/p
=z/p  x
x  p
p  y
y  x
x  p
p  y
y  z,
z,
 =p
=p 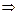 x
x  z
z  y
y  p
p  z/x
z/x  z
z  y,
y,
 =x
=x  p
p  z
z  y
y  z
z  p/x
p/x  z
z 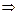 x,
x,
 =x
=x  z
z  p/y
p/y  z
z  p
p  y
y  x
x  z,
z,
 =x
=x  z
z  p
p  y/x
y/x  p
p  x
x  y
y  z,
z,
 =y
=y  p
p  x/z
x/z  y
y  p
p  x
x  z
z  x,
x,
 =p
=p  x
x  y/z
y/z  p
p  x
x  z
z  y
y 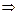 z,
z,
 =x
=x  y
y  z
z  p
p  z
z  y/z
y/z  p
p  x,
x,
 =y/z
=y/z  x
x  p
p  x
x  z
z  y
y  z
z  p,
p,
 =x
=x  y
y  z
z  x
x  y
y  p
p 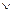 z
z  y/x,
y/x,
 =z
=z  p
p  x
x  (p
(p  z)/z
z)/z  y
y  p
p  x,
x,
 =p/x
=p/x  z
z  y
y  x
x  p
p  z
z  y
y  x,
x,
 =x
=x  y
y  z
z  p
p  x
x 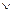 y
y  z/p
z/p  x,
x,
 =z
=z  p
p  x
x  y
y  z
z  p
p  x
x  y/x,
y/x,
 =p
=p  x
x  z
z  y/p
y/p  x
x  y
y  p
p  x,
x,
 =y
=y  x
x  z
z  p/y
p/y  x
x  p
p  z,
z,
 =y
=y  x
x  y
y  p
p  z/x
z/x  y
y  x
x  z,
z,
 =x
=x  y
y  z
z  p
p  x
x  z
z  y
y  p/x,
p/x,
 =z/y
=z/y  p
p  x
x  y
y  z
z  x
x  p
p  y,
y,
 =y
=y  x
x  p
p  z
z  x
x  y/z
y/z  p
p  z,
z,
 =p
=p  x
x  z
z  y
y  x
x  z/p
z/p 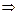 y
y  x,
x,
 =x
=x  y
y  z
z  p/x
p/x  y
y 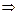 z
z  p
p 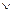 x,
x,
|
 =x
=x  y
y  z
z  p/x
p/x  y
y  z
z  p
p  x,
x,
Функции дизъюнкции и конъюнкции могут быть выражены через импликацию следующим образом:
 (1 – 19)
(1 – 19)
Для функций Шеффера и Вебба имеет место переместительный закон:
 ;
;  .
.
Сочетательный закон для них несправедлив:
 ;
; 
Имеют место следующие очевидные соотношения:
 (1 – 20)
(1 – 20)
Выражение функции Шеффера и Вебба в базисе {  }:
}:
 (1 – 21)
(1 – 21)
Функции Шеффера и Вебба связаны между собой соотношениями, аналогичными формулам де Моргана для функций конъюнкции и дизъюнкции:
 (1 – 22)
(1 – 22)
 2020-07-12
2020-07-12 204
204








