Линейность ФАЛ 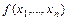 можно определить с помощью разложения в полином Жегалкина в базисе
можно определить с помощью разложения в полином Жегалкина в базисе  .
.
Теорема 7. Всякая ФАЛ 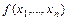 представима полиномом Жегалкина:
представима полиномом Жегалкина:
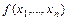
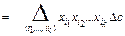 , (1 – 25)
, (1 – 25)
где в каждом наборе 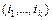 все
все 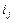 различны, а суммирование ведется по некоторому множеству таких несовпадающих наборов. Представление ФАЛ в виде полинома Жегалкина единственно с точностью до порядка слагаемых.
различны, а суммирование ведется по некоторому множеству таких несовпадающих наборов. Представление ФАЛ в виде полинома Жегалкина единственно с точностью до порядка слагаемых.
Полином Жегалкина называется нелинейным (линейным), если он (не) содержит произведения переменных.
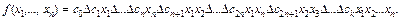 (1 – 26)
(1 – 26)
Линейность ФАЛ равносильна линейности соответствующего полинома Жегалкина.
Для получения полинома Жегалкина заданной ФАЛ 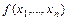 необходимо представить функцию в СДНФ, а далее применить эквивалентности:
необходимо представить функцию в СДНФ, а далее применить эквивалентности:

Пример 1-13. Записать в виде полинома Жегалкина функцию:
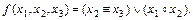

|
16. Показать неполноту следующих систем функций и сделать выводы о существенности условий теоремы Поста:
а) 0, 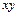 ,
, 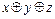 ; б) 1,
; б) 1, 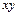 ,
, 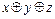 ; в)
; в)  ; г)0, 1,
; г)0, 1, 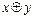 ;
;
д) 0,1, 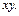
17. Доказать, что ни один из классов 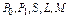 не содержится в другом.
не содержится в другом.
18. Доказать, что всякий собственный функционально замкнутый класс содержится в одном из классов  .
.
19. Доказать, что функционально замкнутые классы 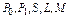 являются предполными и других предполных классов нет.
являются предполными и других предполных классов нет.
Теорема Поста позволяет выяснить вопрос о том, является ли полная система базисом. Это удобно делать при помощи таблиц Поста.
Сделаем некоторые общие замечания о базисах, следующие из теоремы Поста. Начнем с наиболее простого:
20. Доказать, что базис не может содержать более пяти функций.
На самом деле имеет место более точный результат.
21. Доказать, что базис не может содержать более четырех функций.
В силу задач 2 и 9 существуют базисы с любым числом функций, не превосходящим четырех.
22. Доказать, что из всякого базиса можно отождествлением аргументов у входящих в него функций получить базис, в котором все функции зависят не более чем от трех переменных; дальнейшее уменьшение числа переменных, вообще говоря, невозможно.
Определение 14. Если при любом отождествлении переменных у всякой функции базиса получаем неполную систему, то базис называется минимальным.
23. Доказать, что имеется конечное число различных минимальных базисов.
Оказывается, что это число равно 48.
Исследуем некоторые специальные типы базисов. Начнем с базисов, состоящих из одной функции.
Определение 15. Функция алгебры логики, представляющая собой базис из одного элемента, называется обобщенной функцией Шеффера.
24. Сколько имеется обобщенных функций Шеффера от  переменных?
переменных?
25. Найти все минимальные базисы из одной функции.
Теперь, напротив, рассмотрим базисы, содержащие максимально возможное число функций.
26. Какой может быть таблица Поста для базиса из четырех функций?
27. Найти все минимальные базисы из четырех функций.
|
Пример 1-11. Найти  в СПНФ по исходной СДНФ.
в СПНФ по исходной СДНФ.

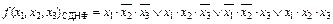
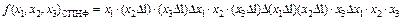
Окончательно после раскрытия скобок и сокращения одинаковых слагаемых, входящих четное число раз, имеем 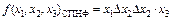 .
.
 2020-07-12
2020-07-12 204
204








