Задача 1. Игральная кость подбрасывается один раз. Наблюдаемый результат – выпавшее число очков. Рассмотрим события:
 – выпавшее число кратно трем;
– выпавшее число кратно трем;  – выпавшее число нечетно;
– выпавшее число нечетно;
 – выпавшее число не меньше трех;
– выпавшее число не меньше трех;  – выпавшее число не больше двух.
– выпавшее число не больше двух.
Сформулировать, в чем состоят события:
1)  , 2)
, 2)  ; 3)
; 3) 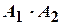 ; 4)
; 4)  ; 5)
; 5)  .
.
Задача 2. События  – появление четного числа очков при бросании игральной кости,
– появление четного числа очков при бросании игральной кости,  – появление двух очков,
– появление двух очков,  – появление четырех очков,
– появление четырех очков,  – появление шести очков. Определить, каким событиям из этого списка равносильны следующие события:
– появление шести очков. Определить, каким событиям из этого списка равносильны следующие события:
1)  ; 2)
; 2)  ; 3)
; 3) 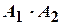 ; 4)
; 4)  .
.
Задача 3. Три студента независимо друг от друга решают одну и ту же задачу. Пусть событие  = {первый студент решил задачу},
= {первый студент решил задачу},  = {второй студент решил задачу},
= {второй студент решил задачу},  = {третий студент решил задачу}. Выразить через
= {третий студент решил задачу}. Выразить через 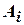 (
( ) следующие события:
) следующие события:  - задачу решил хотя бы один студент;
- задачу решил хотя бы один студент;  - задачу решил только первый студент;
- задачу решил только первый студент;  - задачу решил только один студент.
- задачу решил только один студент.
Тема 2. Классическое, геометрическое и статистическое определения вероятности
Теоретический материал
Основные понятия
§ Исход, благоприятствующий наступлению события  – исход испытания, появление которого влечет за собой наступление события
– исход испытания, появление которого влечет за собой наступление события  .
.
§ Вероятность появления события  – число, равное отношению числа (
– число, равное отношению числа (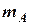 ) элементарных исходов, благоприятствующих наступлению этого события, к общему числу (
) элементарных исходов, благоприятствующих наступлению этого события, к общему числу (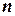 ) всех единственно возможных и несовместных исходов испытания:
) всех единственно возможных и несовместных исходов испытания: 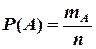 .
.
§ Относительная частота события  – отношение числа (
– отношение числа ( ) испытаний, при которых событие наступило, к общему числу (
) испытаний, при которых событие наступило, к общему числу (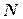 ) проведенных испытаний:
) проведенных испытаний:  .
.
§ Статистическая вероятность события  – относительная частота этого события, вычисленная по результатам большого числа испытаний:
– относительная частота этого события, вычисленная по результатам большого числа испытаний:
 .
.
§ Геометрическая вероятность события  – число, равное отношению меры
– число, равное отношению меры  области события
области события  к мере области пространства элементарных событий
к мере области пространства элементарных событий  :
: 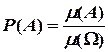 .
.
Свойства вероятности
1. Вероятность достоверного события равна 1:  .
.
2. Вероятность невозможного события равна 0:  .
.
3. Вероятность случайного события есть положительное число, заключенное между 0 и 1:  .
.
4. Сумма вероятностей противоположных событий равна 1:  .
.
Примеры решения задач
 2020-07-12
2020-07-12 311
311








