СЛАЙД 35. Итак, для исследования устойчивости линейной системы достаточно найти корни ее характеристического полинома. Если все корни имеют отрицательные вещественные части (находятся в левой полуплоскости, слева от мнимой оси), такой полином называется устойчивым, потому что соответствующая линейная система устойчива. Полиномы, имеющие хотя бы один корень с положительной вещественной частью (в правой полуплоскости) называются неустойчивыми.
Критерий Гурвица
Существует несколько алгоритмов, позволяющих проверить устойчивость полинома
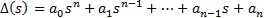 ,
,
не вычисляя его корни. Прежде всего, для устойчивости все коэффициенты 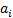 (
(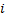 =0,...,n) должны быть одного знака, обычно считают, что они положительные. Это необходимое условие устойчивости полинома. Однако при
=0,...,n) должны быть одного знака, обычно считают, что они положительные. Это необходимое условие устойчивости полинома. Однако при 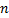 >2 это условие недостаточно, если полином имеет комплексно-сопряженные корни. Поэтому были разработаны необходимые и достаточные условия (критерии) устойчивости полиномов.
>2 это условие недостаточно, если полином имеет комплексно-сопряженные корни. Поэтому были разработаны необходимые и достаточные условия (критерии) устойчивости полиномов.
Один из самых известных критериев - критерий Гурвица - использует матрицу 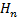 размером
размером 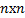 , составленную из коэффициентов полинома
, составленную из коэффициентов полинома 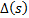 следующим образом:
следующим образом:
• первая строка содержит коэффициенты 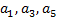 ,... (все с нечетными номерами), оставшиеся элементы заполняются нулями;
,... (все с нечетными номерами), оставшиеся элементы заполняются нулями;
• вторая строка содержит коэффициенты 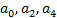 ,... (все с четными номерами);
,... (все с четными номерами);
• третья и четвертая строка получаются сдвигом первой и второй строк на 1 позицию вправо, и т. д.
Например, для полинома 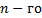 порядка (
порядка (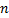 =5) эта матрица имеет вид
=5) эта матрица имеет вид
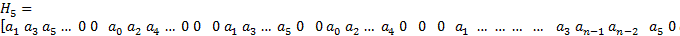 Всегда
Всегда 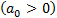
Отчеркивая в главном определители Гурвица, диагональные миноры, получим определитель Гурвица низшего порядка:
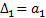
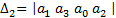
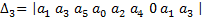
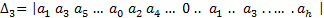
Номер определителя Гурвица определяется номером коэффициента по диагонали, для которого составляют данный определитель. Последний определитель включает в себя всю матрицу. Но так как в последнем столбце все элементы кроме нижнего, равны нулю, то последний определитель Гурвица выражается через предпоследний следующим образом
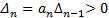
Однако в неустойчивой системе предпоследний определитель тоже должен быть положительным. Поэтому условие положительности последнего определителя сводится к условию 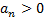 , т. е. к положительности свободного члена характеристического уравнения.
, т. е. к положительности свободного члена характеристического уравнения.
Критерий Гурвица. Для того чтобы система автоматического управления была устойчива, необходимо и достаточно, чтобы все определители Гурвица имели знаки, одинаковые со знаком первого коэффициента характеристического уравнения 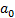 , т. е. при
, т. е. при 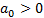 были положительны.
были положительны.
СЛАЙД 36. Раскрывая определители, фигурирующие в общей формулировке критерия устойчивости Гурвица, можно получить в виде частных случаев критерии устойчивости для системы 1-го, 2-го, 3-го, 4-го и более высоких порядков.
1. Уравнение 1-го порядка: 
Для этого уравнения критерий Гурвица дает: 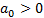 ,
, 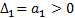 , т.е. коэффициенты характеристического уравнения должны быть положительными.
, т.е. коэффициенты характеристического уравнения должны быть положительными.
2. Уравнение 2-го порядка: 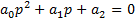
Для этого уравнения критерий Гурвица дает: 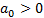 ,
, 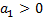 . Последний определитель, как отмечалось выше, сводится к условию положительности последнего коэффициента
. Последний определитель, как отмечалось выше, сводится к условию положительности последнего коэффициента 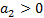 .
.
3. Уравнение 3-го порядка: 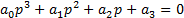
Для этого уравнения получаем условия: 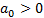 ,
, 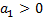 .
. 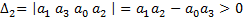
Третий (последний) определитель 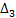 дает условие положительности последнего коэффициента
дает условие положительности последнего коэффициента 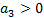 . Условие
. Условие 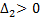 при
при 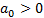 ,
, 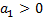 может выполняться только при
может выполняться только при 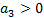 .
.
Следовательно, для уравнения третьего порядка уже недостаточно положительности всех коэффициентов характеристического уравнения. Требуется еще выполнение определенного соотношения между коэффициентами: 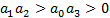
4. Уравнение 4-го порядка: 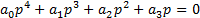
На основании критерия Гурвица можно получить 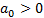 ,
, 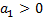 ,
, 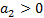 , что для уравнения 4-го порядка, кроме положительности всех коэффициентов требуется выполнение условия:
, что для уравнения 4-го порядка, кроме положительности всех коэффициентов требуется выполнение условия: 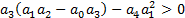
5. Уравнение 5-го порядка: 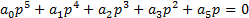
СЛАЙД 37. Для уравнения 5-го порядка, кроме положительности всех коэффициентов требуется выполняться два условия: 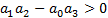
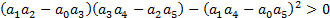
Рассмотрим систему, в которой объект и регулятор задаются передаточными функциями:
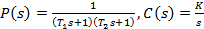 .
.
С помощью критерия Гурвица можно определить, при каких значениях 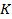 замкнутая система (с отрицательной обратной связью) устойчива. Передаточная функция замкнутой системы равна (10)
замкнутая система (с отрицательной обратной связью) устойчива. Передаточная функция замкнутой системы равна (10) 
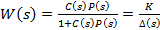 (10)
(10)
где характеристический полином имеет вид (11)
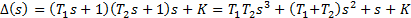 (11)
(11)
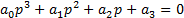 (12)
(12)
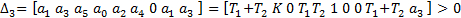 (13)
(13)
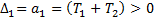 (14)
(14)
СЛАЙД38.
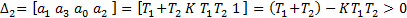 (15)
(15)
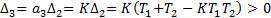 (16)
(16)
Необходимое условие устойчивости дает 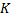 > 0. Применяя критерий Гурвица для системы третьего порядка (), получаем (17)
> 0. Применяя критерий Гурвица для системы третьего порядка (), получаем (17)
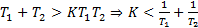 . (17)
. (17)
Таким образом, система устойчива при (18)
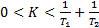 . (18)
. (18)
 2020-08-05
2020-08-05 126
126








