Графо-аналитический метод

Применим графический способ определения параметров передаточной функции.

Общий вид передаточной функции известен: . Время запаздываания было определено ранее. Передаточная функция без запаздывания будет выглядеть: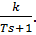  

Для этой передаточной функции известен общий вид переходной функции: .

Найдем производную данного выражения: .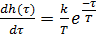

Найдем первый предел полученного выражения: .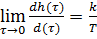

Исходя из геометрического смысла первой производной: . Где 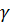 – угол наклона касательной к переходной функции в точке ее начала.

Для применения графического метода на графике переходной функции сделаем дополнительные построения:              

Рис. 10. График переходной функции

Из графика следует:

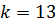
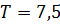
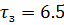
В параметрическом виде передаточная функция запишется

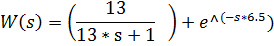
Сведем полученные в результате идентификации данные в таблицу:

Таблица 4.Результаты идентификации

Методы идентификации	Параметры передаточной функции
	K	T
Применение Curve Fiting	13	13	6.5
Применение Identification Toolbox	13	12,9988	6.5
Графический метод	13	7,5	6.5

Анализ дисперсии

Проведем сравнение полученных результатов с исходными данными. Критерием сравнения считаем среднее квадратическое отклонение (СКО). Для того чтобы получить СКО, необходимо получить значение диссперсий для отклонения оценок передаточной функции от исходных данных. Дисперсия в непрерывном варианте расчитывается по формуле:  ; где: ;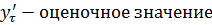

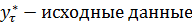
Формула верна для стационарных, эргодических, центрированных случайных процесов. СКО расчитывается по формуле 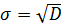. Для дискретного процесса с постоянным тактом дискретности дисперсия будет расчитана по формуле: .

Для расчета СКО построим S-модель.

Рис. 11. S-модель вычисления средних квадратических отклонений.