Непосредственное интегрирование
Функция F (х) называется первообразной для функции f (x), если F ¢ (x) = f (x) или dF (x) = f (x) dx. Если функция f (x) имеет первообразную F(х), то она имеет бесконечное множество первообразных, причем все первообразные содержатся в выражении
F (х) + С,
Где С – постоянная.
Неопределенным интегралом от функции f (x) (или от выражения f (x) dx) называется совокупность всех ее первообразных. Обозначение: 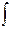 f (x) dx = F (х)+C. Здесь ò - знак интеграла, f (x) – подынтегральная функция, f (x) dx – подынтегральное выражение, х – переменная интегрирования.
f (x) dx = F (х)+C. Здесь ò - знак интеграла, f (x) – подынтегральная функция, f (x) dx – подынтегральное выражение, х – переменная интегрирования.
Отыскание неопределенного интеграла называется интегрированием функции.
Свойства неопределенного интеграла:
1°. (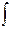 f (x) dx)¢ = f (x).
f (x) dx)¢ = f (x).
2°. d (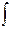 f (x) dx) = f (x) dx.
f (x) dx) = f (x) dx.
3°. 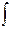 dF (x) = F (х) + C.
dF (x) = F (х) + C.
4°. 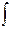 af (x) dx = a
af (x) dx = a 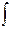 f (x) dx, где а – постоянная.
f (x) dx, где а – постоянная.
5°. 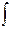 [ f1 (x) ± f2 (x)] dx =
[ f1 (x) ± f2 (x)] dx = 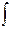 f1 (x) dx ±
f1 (x) dx ± 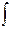 f2 (x) dx.
f2 (x) dx.
6°. Если 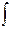 f (x) dx = F (x) + C и u = j (x), то
f (x) dx = F (x) + C и u = j (x), то 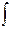 f(u) du = F (u) + C
f(u) du = F (u) + C
Таблица основных неопределенных интегралов:
1. 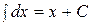 . 7.
. 7. 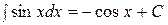 .
.
2. 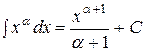 . 8.
. 8. 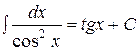 .
.
3.  . 9.
. 9.  .
.
4. 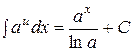 . 10.
. 10. 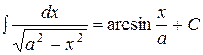 .
.
5. 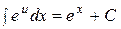 . 11.
. 11. 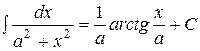 .
.
6. 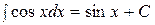 . 12.
. 12. 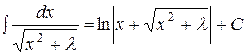 .
.
13. 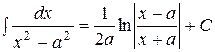 .
.
Пример 44. Найти интеграл 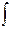 (x3- 5x2 + 7x - 3) dx.
(x3- 5x2 + 7x - 3) dx.
Решение. Используя свойства 4° и 5°, получаем
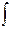
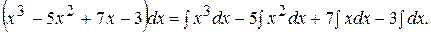
К первым трем интегралам правой части применим формулу (2), а к четвертому интегралу – формулу (1) таблицы интегралов:
 Пример 45. Найти интеграл
Пример 45. Найти интеграл 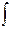 (
(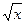 +
+  )
) 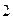
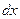 .
.
Решение:
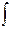 (
(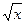 +
+  )2
)2 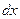 =
= 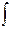 (
(
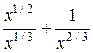 )
) 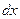 =
= 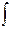 (
(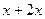
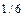
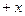
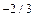 )
) 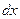 =
=
= 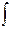
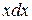
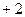
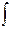

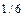
 +
+ 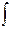

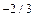
 =
= 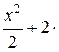
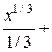
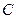 =
= 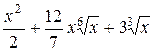 +С.
+С.
 2020-08-05
2020-08-05 78
78








