Двойные интегралы
Пусть функция f(x,y) определена в ограниченной замкнутой области D плоскости хОy. Разобьём область D произвольном образом на n элементарных областей, имеющих площадь ∆σ 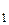 , ∆σ
, ∆σ 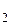 , …, ∆σ
, …, ∆σ  и диаметры d
и диаметры d 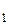 , d2, …, d
, d2, …, d 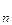 (диаметром области называется наибольшее из расстояний между двумя точками границы этой области). Выберем в каждой элементарной области произвольную точку P
(диаметром области называется наибольшее из расстояний между двумя точками границы этой области). Выберем в каждой элементарной области произвольную точку P 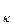 (ξ
(ξ 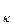 ;ηк) и умножим значение функции в точки P
;ηк) и умножим значение функции в точки P 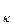 на площадь этой области.
на площадь этой области.
Интегральной суммой для функции f(x,y) по области D называется сумма вида
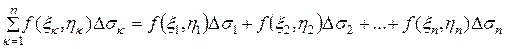 .
.
Если при max d 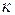
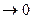 интегральная сумма имеет определенный конечный предел
интегральная сумма имеет определенный конечный предел
I = 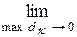
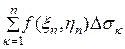 ,
,
не зависящий от способа разбиения D на элементарные области и от выбора точек P 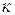 в пределах каждой из них, то этот предел называется двойным интегралом от функции f(x, y) в области D и обозначается следующим образом:
в пределах каждой из них, то этот предел называется двойным интегралом от функции f(x, y) в области D и обозначается следующим образом:
I = 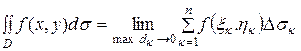 .
.
Если f(x,y)>0 в области D, то двойной интеграл 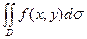 равен объему цилиндрического тела, ограниченного сверху поверхностью z = f(x,y), сбоку цилиндрической поверхностью с образующими, параллельными оси О
равен объему цилиндрического тела, ограниченного сверху поверхностью z = f(x,y), сбоку цилиндрической поверхностью с образующими, параллельными оси О 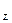 , и снизу областью D плоскости хОy.
, и снизу областью D плоскости хОy.
Основные свойства двойного интеграла:
1. 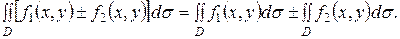
2. 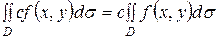 , где с – постоянная.
, где с – постоянная.
3. Если область интегрирования D разбита на две области D 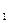 и D
и D 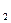 , то
, то
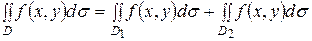
4. Оценка двойного интеграла. Если m ≤ f(x,y) ≤ M, то 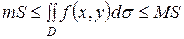 , где S - площадь области D, а m и M – соответственно наименьшее и наибольшее значения функции f(x,y)в области D.
, где S - площадь области D, а m и M – соответственно наименьшее и наибольшее значения функции f(x,y)в области D.
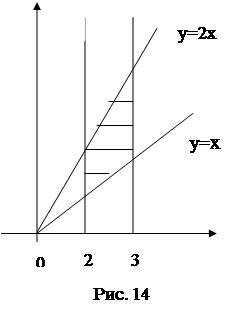
Пример 74. Вычислить 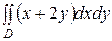 ,если область D ограничена прямыми y = х, y = 2х, х =2, х =3.
,если область D ограничена прямыми y = х, y = 2х, х =2, х =3.
Решение. Вначале построим заданную область D (рис.14). Как видно
из графика
D = 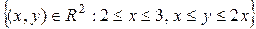 .
.
Тогда 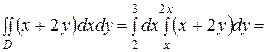
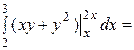
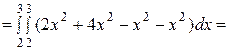
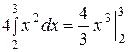 = 25
= 25  .
.
Пример 75. Изменить порядок интегрирования в интеграле:
I 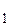 =
= 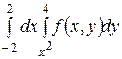 .
.
Решение. Вначале по пределам интегрирования определяем область интегрирования. Полагая x равным пределам интеграла с переменной х, а y равным пределам интеграла с переменной y, получим уравнения линий, ограничивающих эту область: х = -2, х = 2, y = 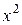 , y = 4.
, y = 4.
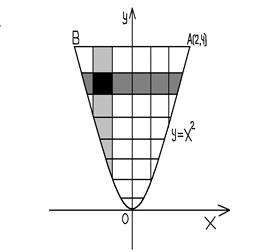 Построив эти линии, получим параболический сегмент ОАВ, симметричный оси О
Построив эти линии, получим параболический сегмент ОАВ, симметричный оси О 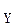 (рис.15).
(рис.15).
Интегрируем в другом порядке – вначале по х, затем по y. Пределы внутреннего интеграла находим, разрешая относительно х
уравнение параболы х = - 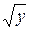 и х =
и х = 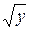 . Пределы внешнего интеграла y = 0 и х = 4 находим как наименьшее и наибольшее значение y во всей области ОАВ. Следовательно,
. Пределы внешнего интеграла y = 0 и х = 4 находим как наименьшее и наибольшее значение y во всей области ОАВ. Следовательно,
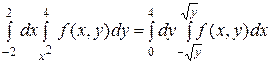 .
.
Рис. 15
Двойной интеграл в полярных координатах. Преобразование двойного интеграла от прямоугольных координат х, y к полярным координатам ρ, θ, связанным с прямоугольными координатами соотношениями
х = r cosj, y = r sinj,
осуществляется по формуле
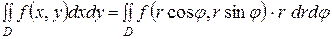 .
.
Пример 76. Перейдя к полярным координатам, вычислить двойной интеграл 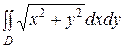 , если D - I четверть круга
, если D - I четверть круга 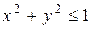 .
.
Решение. Полагая х = r cosj, y = r sinj, имеем уравнение окружности
r2 cos2j + r2 sin2j = 1 или r = 1, тогда
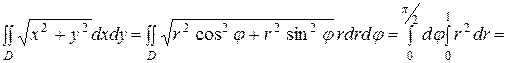 =
= 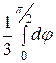 =
= 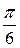 .
.
Вычисление площади плоской фигуры. Площадь плоской фигуры, ограниченной областью D, находится по формуле
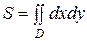 .
.
Если область D определена, например, неравенствами 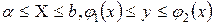 , то
, то
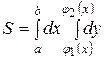 .
.
Если область D в полярных координатах определена неравенствами 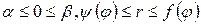 , то
, то
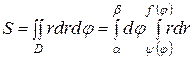 .
.
Пример 77. Вычислить площадь фигуры, ограниченной линиями
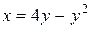 , x + y = 6.
, x + y = 6.
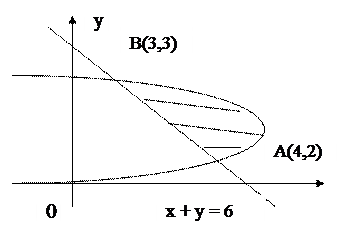
Решение. Построим данную область Д: 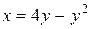 , x + y = 6 (рис.16). Найдем координаты точек пересечения заданных линий, решая систему уравнений:
, x + y = 6 (рис.16). Найдем координаты точек пересечения заданных линий, решая систему уравнений: 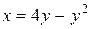 и
и
x + y = 6. В результате получим А(4;2), В(3;3). Таким образом,
D= 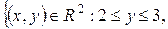
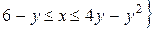 и площадь области равна: Рис. 16
и площадь области равна: Рис. 16
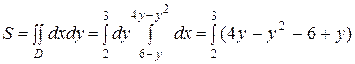 dy =
dy = 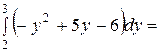
= 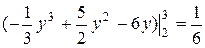 (кв.ед.).
(кв.ед.).
11.2. Криволинейные интегралы
Криволинейный интеграл 1 - го рода. Пусть функция f(x,y) определена и непрерывна в точках дуги АВ гладкой кривой L. Разобьём дугу АВ произвольным образом на n элементарных дуг точками А = А0, А1,…,Аn = В, имеющих длину ∆σ 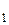 , ∆σ
, ∆σ 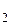 , …, ∆σ
, …, ∆σ 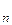 . Выберем на каждой элементарной дуге произвольную точку P
. Выберем на каждой элементарной дуге произвольную точку P 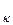 (ξ
(ξ 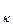 ;ηк) и умножим значение функции в точки P
;ηк) и умножим значение функции в точки P 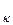 на длину соответствующей дуги.
на длину соответствующей дуги.
Интегральной суммой для функции f(x,y) по длине дуги АВ называется сумма вида
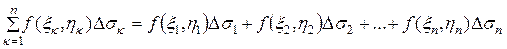 .
.
Если при max s 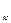
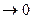 интегральная сумма имеет определенный конечный предел
интегральная сумма имеет определенный конечный предел
I = 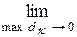
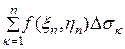 ,
,
то этот предел называется криволинейным интегралом по длине дуги АВ от функции f(x, y) и обозначается следующим образом:
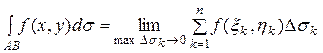 .
.
Если кривая задана уравнением у = j(х) (а £ х £ в), то
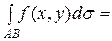
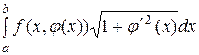 .
.
Если кривая задана параметрическими уравнениями х = х(t), y = y(t) (a£ t £ b), то
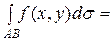
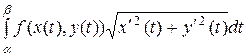 .
.
Основные свойства криволинейного интеграла 1 - го рода:
1. Криволинейный интеграл 1 - го рода не зависит от направления пути интегрирования: 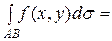
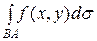 .
.
2. 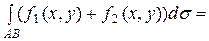
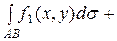
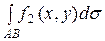 .
.
3. 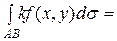 к
к 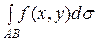 , где к - константа.
, где к - константа.
4. Если К = К1ÈК2, то 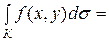
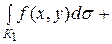
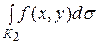 .
.
Пример 78. Вычислить интеграл 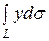 , где L - дуга параболы
, где L - дуга параболы
у2 = 2х от точки (0,0) до точки (4,2 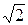 ).
).
Решение. Здесь линию удобно задать в форме, разрешенной относительно х: х = 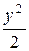 . Тогда х¢ = у и интеграл преобразуется к виду
. Тогда х¢ = у и интеграл преобразуется к виду 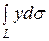 =
= 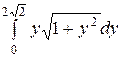 =
= 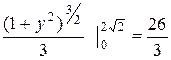 .
.
Криволинейный интеграл 2 - го рода. Пусть функции Р(х,у) и Q(x,y) непрерывны в точках дуги АВ гладкой кривой АВ. Интегральной суммой для функций Р(х,у) и Q(x,y) по координатам называется сумма вида
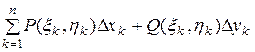 ,
,
где Dк и Dк - проекции дуги на оси Ох и Оу.
Криволинейным интегралом по координатам от выражения Р(х,у)dx+ +Q(x,y)dy по направленной дуге АВ называется предел интегральной суммы при условии, что max Dх 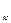
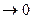 и max Dу
и max Dу 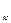
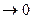 :
:
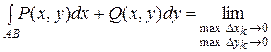
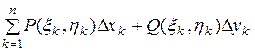 .
.
Если кривая задана уравнением у = j(х) (а £ х £ в), то
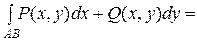
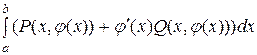 .
.
Если кривая задана параметрическими уравнениями х = х(t), y = y(t) (a£ t £ b), то
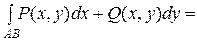
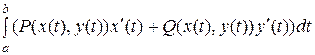 .
.
Основные свойства криволинейного интеграла 2 - го рода. Криволинейный интеграл 2 - го рода меняет знак на противоположный при изменении направления пути интегрирования:
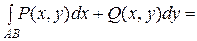
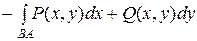 .
.
Остальные свойства аналогичны свойствам интеграла 1 - го рода.
Пример 79. Вычислить интеграл 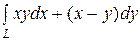 , принимая за линию L:
, принимая за линию L:
1) отрезок прямой, соединяющий точки О (0,0) и А(1,1);
2) дугу параболы у = х2, соединяющей эти же точки.
Решение:
1. Уравнение линии интегрирования у = х. Следовательно, dy = dx и 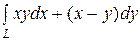 =
= 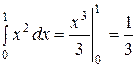 .
.
2. у = х2, dy = 2xdx и 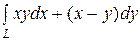 =
= 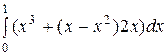 =
= 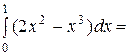
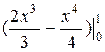 =
=
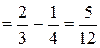 .
.
Криволинейные интегралы по замкнутому множеству обозначим символом 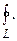 В случае замкнутого контура на плоскости направление обхода, при котором область, ограниченная контуром, остается слева (обход контура совершается против хода часовой стрелки), называется положительным.
В случае замкнутого контура на плоскости направление обхода, при котором область, ограниченная контуром, остается слева (обход контура совершается против хода часовой стрелки), называется положительным.
Формула Грина. Если функции Р(х,у) и Q(х,у) непрерывны вместе со своими частными производными первого порядка в области Д, то имеет место формула
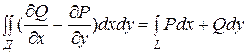 ,
,
где L - граница области Д, и интегрирование вдоль L производится в положительном направлении.
 Пример 80. Применяя формулу Грина, вычислить интеграл
Пример 80. Применяя формулу Грина, вычислить интеграл 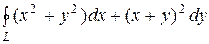 , где L - контур прямоугольника с вершинами
, где L - контур прямоугольника с вершинами
О (0,0), А(5,0), В(5,4) и С(0,4).
Решение. Так как Р(х,у) = х2+у2, Q(x,y) = (х+у)2, то 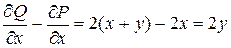 . Таким образом
. Таким образом 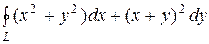 = =
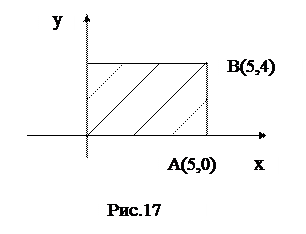
= = 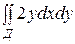 = I, Д - область прямоугольника ОАВС (рис.17).
= I, Д - область прямоугольника ОАВС (рис.17).
Вычислим двойной интеграл по данной области Д:
Д= 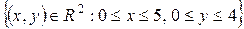 . I=
. I= 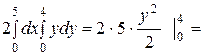
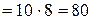 .
.
 2020-08-05
2020-08-05 124
124








