Коническая поверхность вращения

Конической поверхностью называется поверхность, образованная движением прямой АВ, перемещающейся в пространстве через неподвижную точку S и пересекающей кривую линию MN. Прямая АВ называется образующей, линия MN – направляющей, а точка S – вершиной конической поверхности (рис.4).

Рис.4

Конусом (рис.5) называется тело, ограниченное частью конической поверхности, расположенной по одну сторону от вершины, и плоскостью, пересекающей все образующие по ту же сторону от вершины.

Рис. 5 Рис. 6

Конус можно рассматривать как тело, образованное вращением прямоугольного треугольника вокруг катета, принятого за ось вращения. Сечение прямого кругового конуса плоскостью, перпендикулярной к его оси, есть круг (рис. 6).

Проецирование прямого кругового конуса с вертикальной осью (рис. 7) аналогично проецированию пирамиды. В основании конуса будет окружность, с которой следует начинать чертёж. Если ось конуса перпендикулярна горизонтальной плоскости проекций, горизонтальная проекция будет в виде круга, а фронтальная и профильная – в виде треугольников с вершиной S.

Рис. 7

Рис.8,а

Фронтальный очерк конической поверхности (рис. 8,а) определяется проекцией главного меридиана, т.е. проекциями прямолинейных образующих ι´ и ι, расположенных в секущей плоскости α║ П₂. Секущая плоскость β║П₃(рис. 8,б) рассекает конус по образующим κ и κ´, профильные проекции которых определяют профильный очерк поверхности.

Рис. 8,б

Профильные проекции ι₃и ι₃´ образующих ι и ι´, а также фронтальные проекции κ₂ и κ₂´ образующих κ и κ´ совпадают с соответствующими проекциями оси вращения i. Горизонтальная проекция поверхности определяется проекцией n₁окружности n – линии ограничения данной поверхности. Это наибольшая из параллелей, которая на П₂ и П₃ проецируется в виде отрезков прямых n₂и n₃, равных её диаметру.

Рис. 9,а

Линии каркаса параллелей и меридианов показаны на рис. 9,а и рис. 9,б. Параллели радиусов r и R, являющихся результатом пересечения конуса с плоскостями γ║ П₁ и ω║ П₁, на П₁ проецируются без искажения.

Рис. 9,б

Если на поверхности конуса дана одна проекция точки, то через неё проводим образующую, соединяющую основание с вершиной, и, найдя все три проекции образующей, переносим на неё с помощью линий связи проекции данной точки. Вместо образующей можно провести вспомогательную параллель и с её помощью найти проекции точки (рис. 10, а и рис. 10, б).

Рис. 10,а

Рис. 10, б

Сечения конуса

Конус является геометрическим телом, которое может иметь в сечении пять различных фигур:

треугольник, если секущая плоскость пересекает конус через вершину по двум образующим (рис. 11,а и рис. 11, б);

окружность, если секущая плоскость параллельна основанию или перпендикулярна оси, а конус прямой круговой (рис.12);

эллипс, если секущая плоскость пересекает все образующие конуса под некоторым углом к основанию конуса (рис.13);

параболу, если секущая плоскость параллельна одной из образующих конуса (рис.14);

гиперболу, если секущая плоскость параллельна оси конуса или параллельна двум его образующим (рис.15).

Для того чтобы облегчить решение некоторых задач, следует применять плоскость не частного, а общего положения, проходящую через вершину.

Проекции сечений строятся обычно по точкам.

Различают две группы точек:

1 группа: опорные точки, которые выделяются особым расположением на поверхности или отношением к плоскостям проекций.

1.1. Точки видимости, расположенные на очерковых образующих поверхности и определяющие границу видимости линии на соответствующей плоскости проекций.

1.2. Точки экстремальные, т.е. точки минимального или максимального удаления от плоскости проекций.

2 группа: Точки промежуточные или случайные, уточняющие проекции кривой на чертеже.

Все опорные и промежуточные точки плоского сечения строятся с использованием их принадлежности линии данной поверхности.

Рис.11,а Рис.11,б

Рис.12 Рис.13

Рис.14 Рис.15

Эллипс

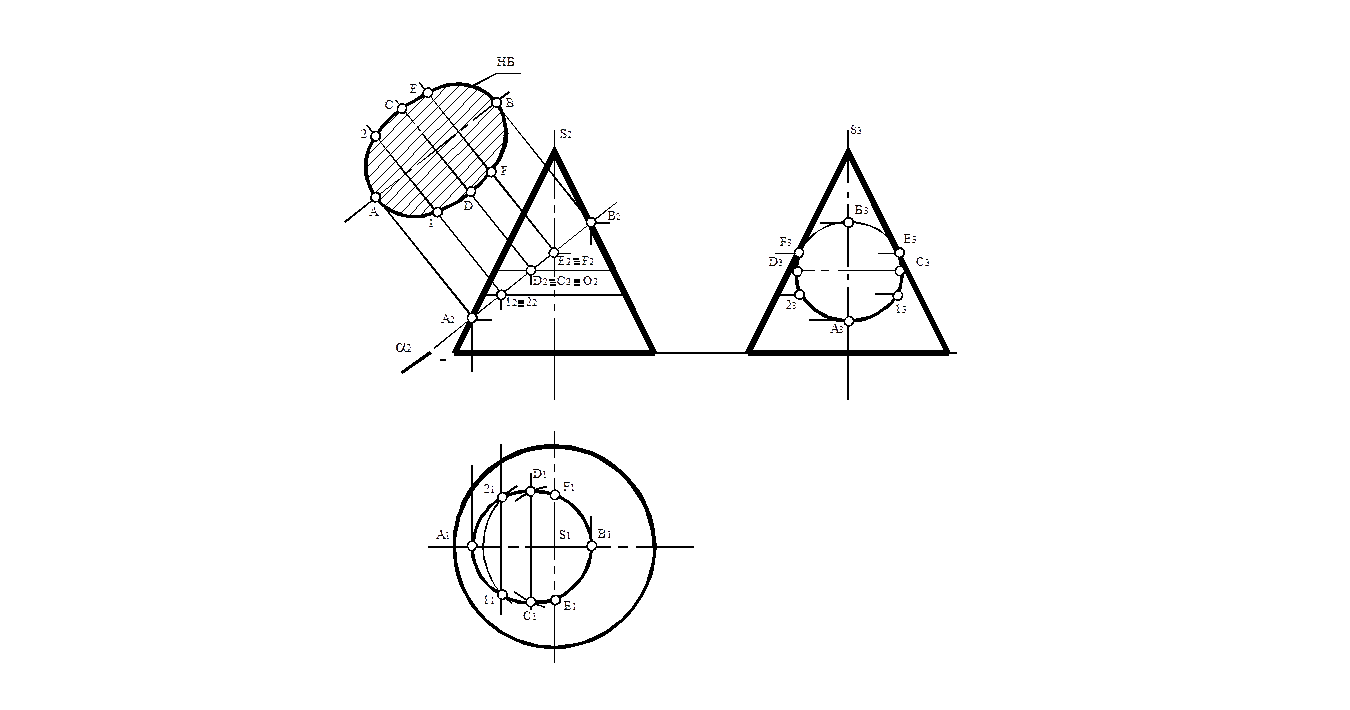Задача. Построить ортогональные проекции и натуральную величину сечения конуса плоскостью α _┴П₂ (рис.16)

Рис.16

Анализ:

1. Фигурой сечения является эллипс, т.к. плоскость α пересекает все образующие конуса и не перпендикулярна к оси вращения.

2. Сечение симметрично относительно плоскости σ║П₂, проходящей через ось вращения конуса. Поэтому одной (двойной) точке фронтальной проекции эллипса соответствуют две симметричные точки горизонтальной и профильной проекций.

3. Фронтальной проекцией эллипса является отрезок прямой линии, совпадающий с вырожденной проекцией секущей плоскости.

4. Горизонтальной и профильной проекциями эллипса в общем случае являются эллипсы.

Решение:

1. Натуральная величина большой оси эллипса определяется отрезком А₂В₂ следа секущей плоскости α, заключённым между фронтальными очерковыми образующими поверхности. Прямая АВ является фронталью.

2. Находим середину отрезка А₂В₂. Она определяет фронтальную проекцию О₂ центра эллипса и вырожденную проекцию малой оси CD.

3. Строим горизонтальные проекции точек С и D, принадлежащих данной поверхности. Отрезок СD является горизонталью, и потому его проекция С₁D₁определяет натуральную величину малой оси эллипса.

4. Определяем точки Е и F эллипса, расположенные на профильных очерковых образующих поверхности конуса. Точки Е и F являются границей видимости кривой на профильной плоскости проекций.

5. Определяем промежуточные точки 1 и 2 с помощью параллели конической поверхности.

6. Выполняем окончательную обводку проекций эллиптического сечения с учётом его видимости.

7. Строим натуральную величину эллипса методом замены плоскостей проекций.

Рис.17

На рис. 17 показано построение неполного эллипса, когда секущая плоскость β пересекает основание конуса по прямой. Рис. 18 даёт изображение конуса, усеченного такой же плоскостью β, поэтому на профильной проекции вся кривая является видимой. Для наглядности плоскость среза, ограниченная эллипсом, показана заштрихованной.

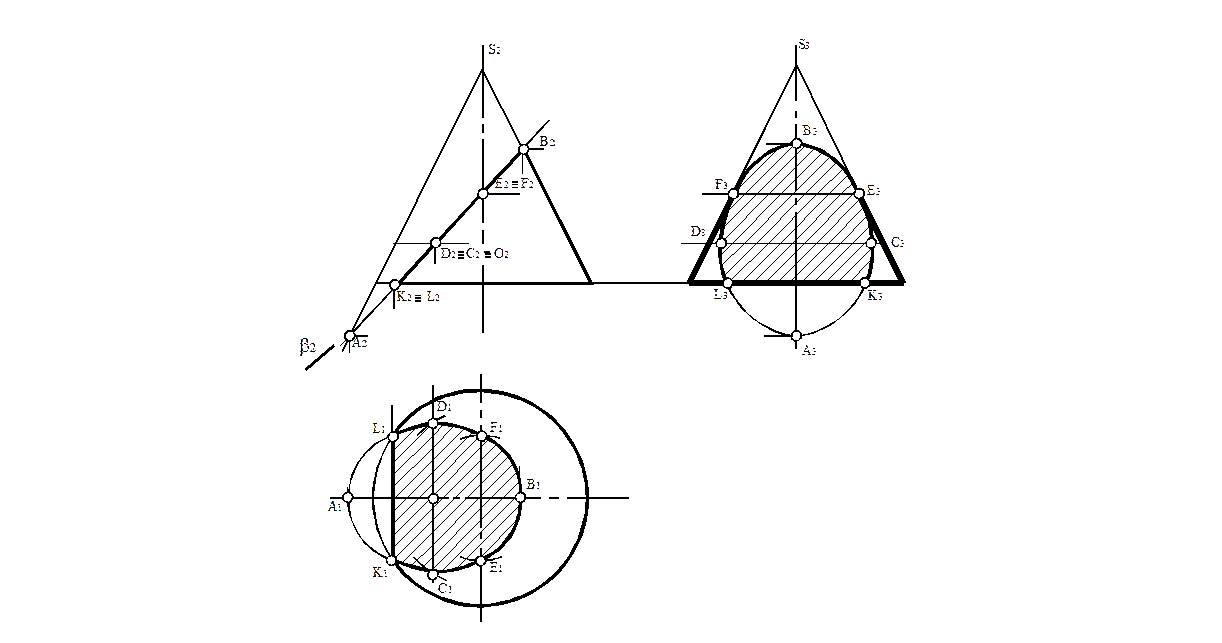
Рис.18

Парабола

Задача. Построить ортогональные проекции и натуральную величину поверхности конуса плоскостью γ_┴П₂, γ║l (рис. 19).

Рис.19

Анализ:

1. Фигура сечения является параболой, т.к. секущая плоскость парал -

лельна одной образующей.

2. Сечение симметрично относительно плоскости σ║П₂ и проходящей

через ось вращения конуса.

3. Фронтальной проекцией параболы является отрезок прямой линии, совпадающей с вырожденной проекцией плоскости γ.

4. На плоскости проекции П₁ и П₃ парабола проецируется в виде параболы.

Решение:

1. Вершина определяется точкой А, расположенной на фронтальной очерковой образующей.

2. На поверхности конуса парабола ограничена точками В и С, принадлежащими окружности основания конуса.

3. Точки D и Е параболы, расположенные на профильных очерковых образующих, определяют границу видимости кривой на профильной плоскости проекций.

4. Точки 1,2,3 и 4 являются промежуточными точками кривой.

5. Натуральная величина фигуры сечения построена методом замены плоскостей проекций.

Гипербола

Задача. Построить ортогональные проекции и натуральную величину сечения поверхности конуса плоскостью τ _┴ П₁ (рис.20).

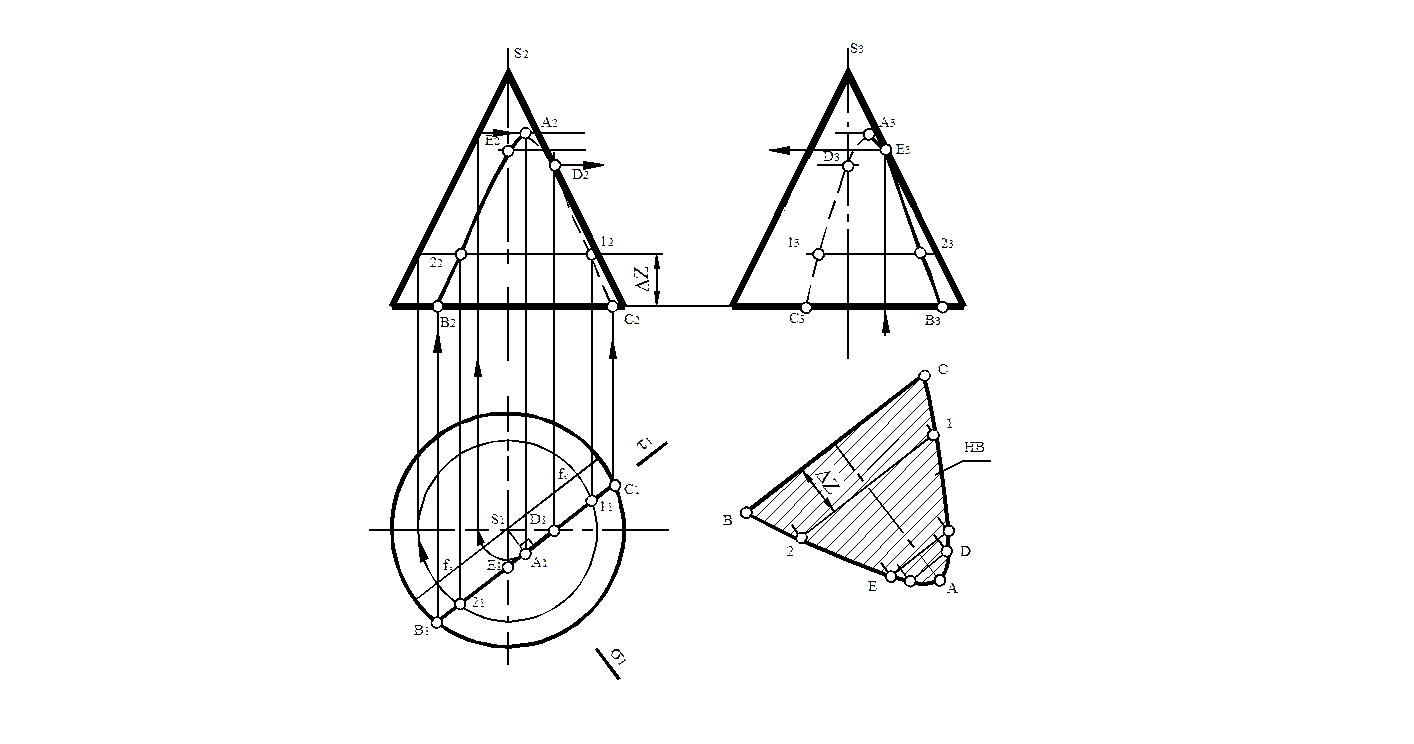
Рис.20

Анализ:

1. Фигура сечения является гиперболой, т.к. секущая плоскость параллельна оси вращения конуса, параллельна и двум его образующим f и f′.

2. Сечение симметрично относительно горизонтально проецирующей плоскости σ_┴ П₁ и проходящей через ось вращения конуса.

3. Горизонтальной проекцией гиперболы является отрезок прямой линии, совпадающей с вырожденной проекцией плоскости τ.

4. На плоскости проекций П₂ и П₃ гипербола проецируется в виде гиперболы.

Решение:

1. Вершина гиперболы А(А₁) определяется как основание перпендикуляра, проведённого из горизонтальной проекции вершины конуса на след секущей плоскости τ.

2. На поверхности конуса гипербола ограничена точками В (В₁) и С (С₁), принадлежащими окружности основания конуса.

3. На пересечении вырожденной проекции секущей плоскости τ с горизонтальными проекциями очерковых k и l′ две точки видимости Е и D. Точка D является границей видимости гиперболы на фронтальной плоскости проекций, точка Е – на профильной.

4. Строим две симметрично расположенные промежуточные точки 1 и 2, принадлежащие одной параллели конуса.

5. Построение натуральной величины фигуры сечения, выполненное методом замены плоскостей проекций, понятно из чертежа.

На рис. 21 имеем чертёж конуса с плоским срезом, фигурой сечения

также является гипербола, т.к. плоскость ω параллельна двум образующим конуса k и k′. Секущая плоскость является профильной, поэтому на П₃ она вырождается в отрезок прямой линии. Построены три опорные точки и четыре промежуточные. На чертеже дано изображение двух ветвей гиперболы.