В теории групп теоремы Си́лова представляют собой неполный вариант обратной теоремы к теореме Лагранжа и для некоторых делителей порядка группы G гарантируют существование подгрупп такого порядка. Теоремы доказаны норвежским математиком Силовом в 1872 г.
Необходимые определения
Пусть 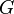 — конечная группа, а
— конечная группа, а 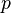 — простое число, которое делит порядок
— простое число, которое делит порядок 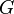 . Подгруппы порядка
. Подгруппы порядка 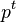 называются
называются 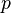 -подгруппами. Выделим из порядка группы
-подгруппами. Выделим из порядка группы 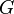 примарный делитель по
примарный делитель по 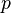 , то есть
, то есть 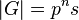 , где
, где  не делится на
не делится на 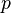 . Тогда силовской
. Тогда силовской 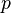 -подгруппой называется подгруппа
-подгруппой называется подгруппа 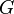 , имеющая порядок
, имеющая порядок 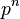 .
.
Теоремы
Пусть 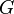 — конечная группа. Тогда:
— конечная группа. Тогда:
- Силовская
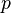 -подгруппа существует.
-подгруппа существует. - Всякая
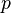 -подгруппа содержится в некоторой силовской
-подгруппа содержится в некоторой силовской 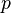 -подгруппе. Все силовские
-подгруппе. Все силовские 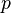 -подгруппы сопряжены (то есть каждая представляется в виде
-подгруппы сопряжены (то есть каждая представляется в виде 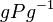 , где
, где 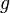 — элемент группы, а
— элемент группы, а 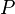 — силовская подгруппа из теоремы 1).
— силовская подгруппа из теоремы 1). - Количество силовских
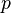 -подгрупп
-подгрупп 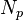 сравнимо с единицей по модулю
сравнимо с единицей по модулю 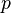 (
(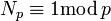 ) и делит порядок
) и делит порядок 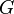 .
.
Следствие
Если все делители 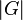 , кроме 1, после деления на
, кроме 1, после деления на 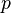 дают остаток, отличный от единицы, то в
дают остаток, отличный от единицы, то в 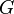 есть единственная силовская
есть единственная силовская 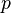 -подгруппа и она является нормальной (и даже характеристической).
-подгруппа и она является нормальной (и даже характеристической).
СОПРЯЖЁННЫЙ ЭЛЕМЕНТ ГРУППЫ
СОПРЯЖЕННЫЙ ЭЛЕМЕНТ к элементу. группы G - элемент х' такой, что
x'=g -1 xg
для нек-рого элемента gиз G. Говорят также, что х' получается на хтрансформированием при помощи элемента g. Для С. э. используется иногда степенное обозначение: xg.
Если А к В два подмножества группы G, то через А B принято обозначать множество
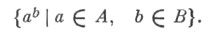
Множество 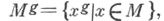 где g - нек-рый фиксированный элемент из G, наз. сопряженным с множеством Мв группе G. В частности, две подгруппы. и Vназ. сопряженными п о д-гр уппами, если U=Vg для нек-рого gиз G. Если подгруппа Н=Н g для любого элемента
где g - нек-рый фиксированный элемент из G, наз. сопряженным с множеством Мв группе G. В частности, две подгруппы. и Vназ. сопряженными п о д-гр уппами, если U=Vg для нек-рого gиз G. Если подгруппа Н=Н g для любого элемента 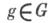 (т. е. Нсодержит все элементы, сопряженные с ее элементами), то Нназ. самосопряженной подгруппой в G,или нормальным делителем.
(т. е. Нсодержит все элементы, сопряженные с ее элементами), то Нназ. самосопряженной подгруппой в G,или нормальным делителем.
КЛАСС СОПРЯЖЁННОСТИ
Класс сопряженных элементов группы F, состоящий из вещественных элементов, называется вещественным. [1]
Это указывает соответствие между классами сопряженных элементов группы % и множествами свободно гомотопных замкнутых геодезических пространства R, если пространство К - прямое. [2]
Если А оставляет неподвижным некоторый класс сопряженных элементов группы Я, то А оставляет на месте некоторый элемент этого класса. [3]
Тогда, если А есть класс сопряженных элементов группы GI, a Л2 - класс сопряженных элементов группы G2, то всевозможные произведения вида а а2, где а А, а2еЛ2, образуют класс сопряженных элементов самой группы G, и обратно, каждый класс сопряженных элементов группы G получается таким образом. [4]
Пусть G H содержится в некотором классе сопряженных элементов группы С. [5]
Все подобные друг другу перестановки вида а0асто, образующие класс сопряженных элементов группы S (N), имеют одинаковую структуру циклов. [6]
Тогда, если А есть класс сопряженных элементов группы GI, a Л2 - класс сопряженных элементов группы G2, то всевозможные произведения вида а а2, где а А, а2еЛ2, образуют класс сопряженных элементов самой группы G, и обратно, каждый класс сопряженных элементов группы G получается таким образом. [7]
Пусть универсальное накрывающее пространство R пространства R - прямое и пусть Sk ь St принадлежит к классу сопряженных элементов группы, определенному классом кривых, свободно гомотопных К. Замкнутая геодезическая (свободно гомотопная К, существует тогда и только тогда, когда Sft есть осевое движение. [8]
Тогда, если А есть класс сопряженных элементов группы GI, a Л2 - класс сопряженных элементов группы G2, то всевозможные произведения вида а а2, где а А, а2еЛ2, образуют класс сопряженных элементов самой группы G, и обратно, каждый класс сопряженных элементов группы G получается таким образом. [9]
Можно считать, что nl - 1, так как единица составляет класс. Элемент af составляет класс сопряженных элементов группы G тогда и только тогда, когда он принадлежит центру Z группы G. [10]
Все элементы одного класса сопряженных элементов, согласно сказанному выше, отвечают одной и той же орбите. Таким образом, устанавливается взаимнооднозначное соответствие между классами сопряженных элементов группы и периодическими орбитами. [11]
Поэтому такой элемент а характеризуется тем фактом, что он коммутирует со всеми элементами х алгебры: ах ха. Применяя термин, перенесенный из теории групп в алгебру, мы можем сказать: те элементы, чьи компоненты зависят только от класса сопряженных элементов группы, содержащего аргу мент s, образуют центр алгебры. [12]
Доказать, что: а-д 5, Ь - Ь, с - с - внешний автоморфизм группы G, который переводит каждый класс сопряженных элементов группы G в себя. [13]
Далее, сумму (8.4.19) можно представить, как сумму по классам сопряженных элементов [ рп ], где индекс р задает все примитивные элементы, а п фиксирует все их повторения, а также элементы каждого класса. Сумма по элементам классов сопряженных элементов может быть вычислена явно. В результате функция Грина будет представлена в виде суммы по классам сопряженных элементов группы, т.е. по примитивным орбитам. [14]
А обозначим через а образ элемента а в группе А при рассматриваемом представлении. Пусть ср - функция, отображающая группу А в некоторое кольцо многочленов над полем рациональных чисел, причем эта функция постоянна на классах сопряженных элементов группы А. Как обычно, функцию ср назовем функцией класса для группы А. Предположим, что группа А имеет. У, взятые по одному из каждой орбиты.
ИДЕАЛ КОЛЬЦА
Для кольца 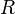 идеалом называется подкольцо, замкнутое относительно умножения на элементы из
идеалом называется подкольцо, замкнутое относительно умножения на элементы из 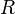 . При этом идеал называется левым (соответственно правым), если он замкнут относительно умножения слева (соответственно справа) на элементы из
. При этом идеал называется левым (соответственно правым), если он замкнут относительно умножения слева (соответственно справа) на элементы из 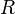 . Идеал, являющийся одновременно левым и правым, называется двусторонним. Двусторонний идеал часто называется просто идеалом. В коммутативном случае все эти три понятия совпадают и всегда применяется термин идеал.
. Идеал, являющийся одновременно левым и правым, называется двусторонним. Двусторонний идеал часто называется просто идеалом. В коммутативном случае все эти три понятия совпадают и всегда применяется термин идеал.
Более точно: Идеалом кольца 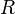 называется такое подкольцо
называется такое подкольцо 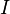 кольца
кольца 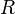 , что
, что
-
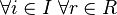 произведение
произведение 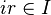 (условие на правые идеалы);
(условие на правые идеалы); -
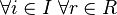 произведение
произведение 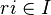 (условие на левые идеалы).
(условие на левые идеалы).
Аналогично для полугруппы её идеалом называется подполугруппа, для которой верно какое-нибудь из этих условий (или оба для двустороннего идеала), то же самое и для алгебры.
Свойства
- Левые идеалы в R являются правыми идеалами в т.н. противоположном кольце
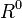 — кольце с теми же элементами и тем же сложением, что и данное, но с умножением определенным
— кольце с теми же элементами и тем же сложением, что и данное, но с умножением определенным 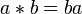 , и наоборот.
, и наоборот. - Двусторонние идеалы в кольцах и алгебрах играют ту же роль, что и нормальные подгруппы в группах:
- Для всякого гомоморфизма
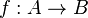 ядром
ядром 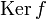 является идеал, и обратно, всякий идеал — ядро некоторого гомоморфизма.
является идеал, и обратно, всякий идеал — ядро некоторого гомоморфизма. - Более того, идеал однозначно (с точностью до изоморфизма) определяет образ гомоморфизма, ядром которого он является:
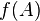 изоморфен факторкольцу (факторалгебре)
изоморфен факторкольцу (факторалгебре) 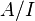 .
. - В кольце
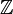 целых чисел все идеалы главные и имеют вид
целых чисел все идеалы главные и имеют вид 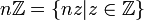 , где
, где 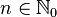 .
. - Пересечение идеалов также является идеалом (часто, особенно в коммутативной алгебре, пересечение называется наименьшим общим кратным).
ГЛАВНЫЙ ИДЕАЛ КОЛЬЦА
Определение
Левый идеал кольца 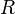 называется главным левым идеалом, если он порождён одним элементом
называется главным левым идеалом, если он порождён одним элементом 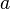 . Аналогично определяются главные правые идеалы и главные двусторонние идеалы.
. Аналогично определяются главные правые идеалы и главные двусторонние идеалы.
Общепринятых обозначений для главных идеалов нет. Иногда используют обозначения 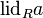 ,
, 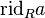 ,
, 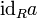 для левых, правых и двусторонних главных идеалов соответственно.
для левых, правых и двусторонних главных идеалов соответственно.
Если 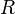 — коммутативное кольцо, то эти три понятия эквивалентны. В этом случае идеал, порождённый
— коммутативное кольцо, то эти три понятия эквивалентны. В этом случае идеал, порождённый 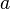 , обозначают через
, обозначают через 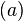 .
.
В случае ассоциативного кольца с единицей главные идеалы описываются следующим образом.
-
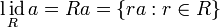 .
. -
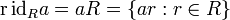 .
. -
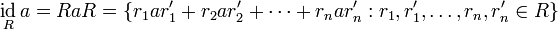 .
.
Если же 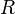 — ассоциативное кольцо (вообще говоря без единицы), то
— ассоциативное кольцо (вообще говоря без единицы), то
-
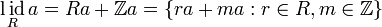 .
. -
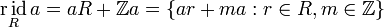 .
. -
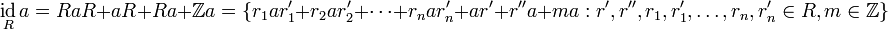 .
.
Не все идеалы — главные. Рассмотрим, например, коммутативное кольцо 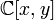 многочленов с комплексными коэффициентами от двух переменных
многочленов с комплексными коэффициентами от двух переменных 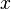 и
и 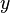 . Идеал
. Идеал 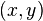 , порождённый многочленами
, порождённый многочленами 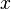 и
и 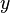 , (то есть идеал состоящий из многочленов, у которых свободный член равен нулю) не будет главным. Чтобы доказать это, допустим, что этот идеал порождается некоторым элементом
, (то есть идеал состоящий из многочленов, у которых свободный член равен нулю) не будет главным. Чтобы доказать это, допустим, что этот идеал порождается некоторым элементом 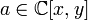 ; тогда на него должны делиться
; тогда на него должны делиться 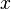 и
и 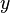 . Это возможно, только если
. Это возможно, только если 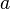 — ненулевая константа. Но в
— ненулевая константа. Но в 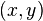 только одна константа — нуль. Приходим к противоречию.
только одна константа — нуль. Приходим к противоречию.
Примеры
Все евклидовы кольца являются областями главных идеалов; в них для поиска порождающего элемента данного идеала можно использовать алгоритм Евклида. Вообще, у любых двух главных идеалов коммутативного кольца есть наибольший общий делитель в смысле умножения идеалов; благодаря этому в областях главных идеалов можно вычислять (с точностью до умножения на обратимый элемент) НОД элементов 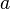 и
и 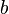 как порождающий элемент идеала
как порождающий элемент идеала 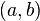 .
.
 2020-08-05
2020-08-05 515
515