Централизатор элемента группы

Централизатор

Максимальная подгруппа, каждый элемент которой коммутирует с заданным элементом: .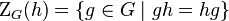

Централизатор элемента (1, 0) в S (g; х) состоит из элементов вида (се, Р) с сех - се. [1]

Вычисление централизаторов элементов (и неподвижных точек автоморфизмов) конечных групп типа Ли основано на другом фундаментальном результате Стейнберга о линейных алгебраических группах G. Рассматривая G как матричную группу, мы называем элемент л: из G полупростым, если он диагонализуется. [2]

Строение централизатора Сх элемента х (порядка 2) в группе типа Рг также объясняет, почему было принято обозначение F2 для группы Фишера, порожденной (3, 4 -транспозициями. [3]

Показать, что централизаторы элементов, не лежащих в F, коммутативны. [4]

Согласно предложению 25.63, централизатор элемента из К F (U25), имеющего по модулю V (К. [5]

Однако для дальнейшего анализа строения централизаторов элементов порядка р важно выяснить взаимосвязь между элементами из Sp (G), встречающимися в L (CjOp (Са)) и в L (СЬ / 0Р (Сь)) для коммутирующих элементов a, b порядка р в G. [6]

Таким образом, для вычисления централизатора а-неподвижного полупростого элемента (или автоморфизма) х конечной группы Х Ga типа Ли мы переходим к соответствующей алгебраической группе G (или к ее односвязной накрывающей) и из общей теории определяем полупростой автоморфизм t группы G, отвечающий х, вычисляем G /, используя предыдущую теорему для описания ее строения, и, наконец, пересекаем получившуюся группу с X. На практике по ходу дела приходится использовать весьма деликатные рассуждения, однако сказанное выше позволяет судить в общих чертах о процедуре. [7]

В § 0.4 рассматриваются так называемые собственные кольца и централизаторы элементов; эти понятия используются в основном в гл. [8]

В этой же главе приводится доказательство теоремы Бергмана о централизаторах элементов свободной алгебры (централизатор нескалярного элемента свободной алгебры изоморфен алгебре многочленов от одной переменной), использующее различные гомоморфизмы свободной алгебры в алгебру многочленов. Что касается других связей излагаемой теории, то уже из беглого просмотра книги можно заметить, что в ней систематически используются теория решеток для изучения разложений элементов на множители и различные сведения и методы (в том числе гомологические) из теории модулей. [9]

Полагая в этой теореме Ь а, мы получаем следующее представление централизатора элемента a. [10]

Если 5 состоит из одного элемента а, то N называют также централизатором элемента а. Тогда Zs называется централизатором подмножества S. Централизатор самой группы G называется ее центром. [11]

Понятно, что многие свойства (такие, как автоморфизмы, сопряженные классы и централизаторы элементов) групп Sp (n, q) и 0е (п, q) можно будет определить, исходя из действия этих групп на V и матричных представлений относительно подходящим образом выбранных базисов, аналогично тому, как это делается в линейном случае. Решающую роль в рассуждениях линейного случая играет тот факт, что любое невырожденное линейное преобразование между подпространствами (/, U из V может быть продолжено до невырожденного линейного преобразования всего пространства V. Аналог этого результата, принадлежащий Витту, столь же фундаментален для исследования симплектических и ортогональных групп. [12]

С G - подгруппа Ли, соответствующая подалгебре Ли д0 С д; это централизатор элемента У при присоединенном действии. [13]

В этой же главе приводится доказательство теоремы Бергмана о централизаторах элементов свободной алгебры (централизатор нескалярного элемента свободной алгебры изоморфен алгебре многочленов от одной переменной), использующее различные гомоморфизмы свободной алгебры в алгебру многочленов. Что касается других связей излагаемой теории, то уже из беглого просмотра книги можно заметить, что в ней систематически используются теория решеток для изучения разложений элементов на множители и различные сведения и методы (в том числе гомологические) из теории модулей. [14]

Стабилизатор элемента X обозначается через ZH (X) мы называем группу ZH (X) централизатором элемента X в Я.