Представление симметрической группы в виде матричной

Любая подгруппа группы перестановок 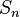представима группой матриц из 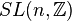, при этом каждой перестановке 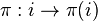соответствует матрица, у которой все элементы в ячейках равны 1, а прочие элементы равны нулю. Например, перестановка 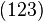представляется следующей матрицей :

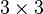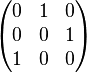
Такие матрицы называются перестановочными

В частности, получаем, что знакопеременная группа 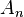- это группа матриц, определитель которых равен 1. Существуют представления симметрических групп меньшей размерности.

ЗНАКОПЕРЕМЕННАЯ ГРУППА

Знакопеременной группой подстановок степени n (обозн. 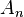) называется подгруппа симметрической группы 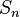степени 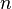, содержащая только чётные перестановки.

Свойства

Индекс подгруппы знакопеременной группы в симметрической равен 2:

Знакопеременная группа является нормальной подгруппой симметрической группы (следует из предыдущего утверждения).
Порядок знакопеременной группы равен:

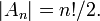
Знакопеременная группа является коммутантом симметрической группы:
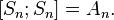
Знакопеременная группа разрешима тогда и только тогда, когда её порядок не больше 4. Точнее, 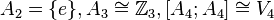- четверной группе Клейна, а при .

ЦИКЛИЧЕСКАЯ ГРУППА

В теории групп группа называется циклической, если она может быть порождена одним элементом a, то есть все её элементы являются степенями a (или, если использовать аддитивную терминологию, представимы в виде na, где n — целое число). Математическое обозначение: .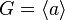

Несмотря на своё название, группа не обязательно должна буквально представлять собой «цикл». Может случиться так, что все степени 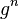будут различными. Порождённая таким образом группа называется бесконечной циклической группой и изоморфна группе целых чисел по сложению ().

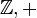Свойства

Все циклические группы абелевы.
Каждая конечная циклическая группа изоморфна группе 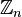— 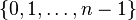со сложением по модулю n (её также обозначают 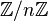), а каждая бесконечная — изоморфна 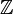, группе целых чисел по сложению.

В частности, для каждого натурального числа n существует единственная (с точностью до изоморфизма) циклическая группа порядка n.

Каждая подгруппа циклической группы циклична.
У циклической группы порядка n существует ровно φ(n) порождающих элементов, где φ — функция Эйлера
Если p — простое число, то любая группа порядка p циклическая и единственна с точностью до изоморфизма (это следует из теоремы Лагранжа).
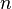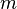Прямое произведение двух циклических групп порядков и циклично тогда и только тогда, когда n и m взаимно просты.

Например, 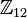изоморфна 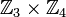, но не изоморфна .

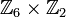Основная теорема о конечнопорождённых абелевых группах утверждает, что любая конечнопорождённая абелева группа единственным образом разлагается в прямое произведение примарных циклических групп. Примарной группой может быть циклическая группа 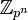, где p — простое число, или .
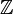Мультипликативная группа любого конечного поля является циклической (она порождается элементом поля наибольшего порядка).
Кольцо эндоморфизмов группы 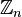изоморфно кольцу 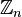. При этом изоморфизме числу r соответствует эндоморфизм 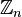, который сопоставляет элементу сумму r его экземпляров. Такое отображение будет биекцией, если и только если r взаимно просто с n, так что группа автоморфизмов 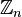изоморфна .

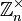Примеры

Группа корней из единицы степени n по умножению.
Группа Галуа любого конечного расширения конечного поля конечна и циклична; обратно, если дано конечное поле F и конечная циклическая группа G, существует конечное расширение F группой Галуа которого будет G.

ФАКТОРГРУППА

Факторгруппа — конструкция, дающая новую группу (факторгруппу) по группе и её нормальной подгруппе.

Факторгруппа группы по нормальной подгруппе 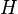обычно обозначается .

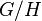Определение

Пусть — группа, и 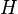— её нормальная подгруппа. Тогда на классах смежности 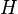в

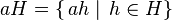
можно ввести умножение:

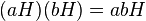
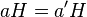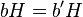Легко проверить что это умножение не зависит от выбора элементов в классах смежности, то есть если и , то 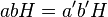. Это умножение определяет структуру группы на множестве классов смежности, а полученная группа 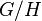называется факторгруппой по .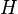

Свойства

Гомоморфный образ группыДо победы коммунизмаИзоморфен факторгруппеПо ядру гомоморфизма.

Теорема о гомоморфизме: Для любого гомоморфизма

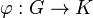
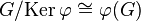то есть факторгруппа по ядру изоморфна её образу 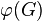в .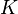

Отображение 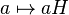задаёт естественный гомоморфизм .
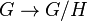Порядок 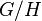равен индексу подгруппы 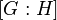. В случае конечной группы он равен .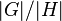
Если абелева, нильпотентна, разрешима, циклическая или конечнопорождённая, то и 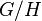будет обладать тем же свойством.
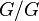изоморфна тривиальной группе (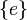), 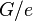изоморфна .

Примеры

Пусть 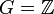, , 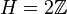тогда 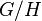изоморфна .

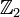Пусть 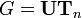(группа невырожденных верхнетреугольных матриц), 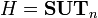(группа верхних унитреугольных матриц), тогда 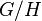изоморфна группе диагональных матриц.

НОРМАЛЬНАЯ ПОДГРУППА

Норма́льная подгру́ппа (также инвариа́нтная подгру́ппа) — подгруппа особого типа, левый и правый смежные классы по которой совпадают. Такие группы важны, поскольку позволяют строить факторгруппу.

Определения

Подгруппа 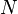группы называется нормальной, если она инвариантна относительно сопряжений, то есть для любого элемента 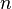из 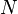и любого 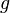из , элемент лежит в :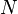

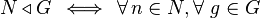
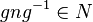
Следующие условия нормальности подгруппы эквивалентны:

Для любого 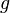из , .
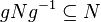Для любого 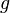из , .
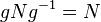Множества левых и правых смежных классо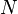в в совпадают.
Для любого 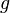из , .
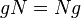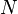изоморфна объединению классов сопряженных элементов.

Условие (1) логически слабее, чем (2), а условие (3) логически слабее, чем (4). Поэтому условия (1) и (3) часто используются при доказательстве нормальности подгруппы, а условия (2) и (4) используются для доказательства следствий нормальности.

Примеры

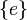и — всегда нормальные подгруппы . Они называются тривиальными. Если других нормальных подгрупп нет, то группа называется простой.

Центр группы — нормальная подгруппа.

Коммутант группы — нормальная подгруппа.

Любая характеристическая подгруппа нормальна, так как сопряжение — это всегда автоморфизм.

Все подгруппы 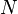абелевой группы нормальны, так как 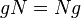. Неабелева группа, у которой любая подгруппа нормальна, называется гамильтоновой.

Группа параллельных переносов в пространстве любой размерности — нормальная подгруппа евклидовой группы; например, в трёхмерном пространстве поворот, сдвиг и поворот в обратную сторону приводит к простому сдвигу.

В группе кубика Рубика подгруппа, состоящая из операций, действующих только на угловые элементы, нормальна, так как никакое сопряжённое преобразование не заставит такую операцию действовать на краевой, а не угловой элемент. Напротив, подгруппа, состоящая лишь из поворотов верхней грани, не нормальна, так как сопряжения позволяют переместить части верхней грани вниз.

Свойства

Нормальность сохраняется при сюрьективных гомоморфизмах и взятии обратных образов.
Ядро гомоморфизма — нормальная подгруппа.
Нормальность сохраняется при построении прямого произведения.
Нормальная подгруппа нормальной подгруппы не обязана быть нормальной в группе, то есть нормальность не транзитивна. Однако характеристическая подгруппа нормальной подгруппы нормальна.
Каждая подгруппа индекса 2 нормальна. Если 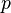— наименьший простой делитель порядка , то любая подгруппа индекса 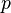нормальна.
Если 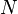— нормальная подгруппа в , то на множестве левых (правых) смежных классов 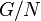можно ввести групповую структуру по правилу

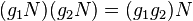
Полученное множество называется факторгруппой по .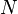

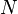нормальна тогда и только тогда, когда она тривиально действует на левых смежных классах .

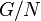ЦЕНТР ГРУППЫ

Центр группы

(математический)

совокупность элементов группы перестановочных со всеми её элементами (т. е. таких элементов z, что zg = gz для всех элементов g из данной группы G). Ц. г. является подгруппой в G, переходящей в себя при всех автоморфизмах. В группе невырожденных матриц порядка n Ц. г. совпадает с подгруппой скалярных матриц (матриц вида λ Е, где λ — число, а Е — единичная матрица).

Центр группы

Максимальная группа элементов, коммутирующих с каждым элементом группы: . Своеобразная «мера абелевости»: группа абелева тогда и только тогда, когда её центр совпадает со всей группой.