Кольцо главных идеалов

Кольцо главных идеалов — кольцо, каждый идеал которого является главным. В случае некоммутативного кольца различают кольцо главных правых идеалов и кольцо главных левых идеалов.

Примеры

Все евклидовы кольца, в том числе, кольцо целых чисел 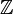, являются кольцами главных идеалов.
Пример кольца, не являющегося кольцом главных идеалов — кольцо многочленов 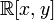. В нём идеал, порождённый 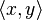не является главным, то есть, не может быть порождён одним элементом кольца.

Свойства

Кольцо главных идеалов является нётеровым.
Все кольца главных идеалов являются кольцами Безу.

СУММА ИДЕАЛОВ

Сумма идеалов. Если в кольце R задано произвольное семейство идеалов 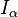, их суммой 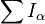называется минимальный идеал, который их всех содержит. Он порождён объединением этих идеалов, и его элементами являются любые конечные суммы элементов из их объединения. (Само объединение идеалов обычно идеалом не является.) Относительно суммы все (левые, правые или двусторонние) идеалы кольца (или алгебры) образуют решётку. Каждый идеал является суммой главных идеалов. Часто, особенно в коммутативной алгебре, сумма называется наибольшим общим делителем).

ФАКТОРКОЛЬЦО

Факторкольцо́ — общеалгебраическая конструкция, позволяющая распространить на случай колец конструкцию факторгруппы. Любое кольцо является группой по сложению, поэтому можно рассмотреть её подгруппу и взять факторгруппу. Однако для того, чтобы на этой факторгруппе можно было корректно определить умножение, необходимо, чтобы исходная подгруппа была замкнута относительно умножения на произвольные элементы кольца, то есть являлась идеалом.

Определение

Пусть 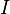— двусторонний идеал кольца 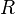. Определим на 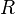отношение эквивалентности:

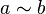тогда и только тогда, когда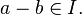

Класс эквивалентности элемента 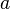обозначается как 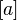или 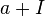и называется классом смежности по модулю идеала. Факторкольцо 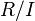— это множество классов смежности элементов 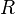по модулю 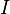, на котором следующим образом определены операции сложения и умножения:

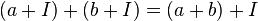
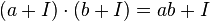
Легко проверить, что эти операции определены корректно, то есть не зависят от выбора конкретного представителя 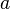класса смежности 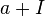. Например, корректность умножения проверяется следующим образом: пусть 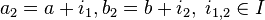. Тогда 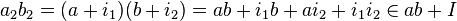. В последнем шаге доказательства использовалась замкнутость идеала относительно умножения на элемент кольца (как слева, так и справа) и замкнутость относительно сложения.

Примеры

Пусть 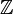— кольцо целых чисел, 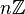— идеал, состоящий из чисел, кратных 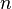. Тогда 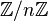— кольцо вычетов по модулю .
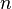Рассмотрим кольцо многочленов с действительными коэффициентами 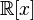и идеал, состоящий из многочленов, кратных 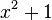. Факторкольцо 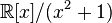изоморфно полю комплексных чисел: класс 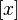соответствует мнимой единице. Действительно, в факторкольце элементы 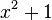и 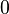эквивалентны, то есть .
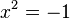Обобщая предыдущий пример, факторкольца часто используют для построения расширений полей. Пусть 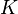— некоторое поле и 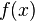— неприводимый многочлен в 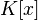. Тогда 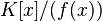является полем, и это поле содержит по крайней мере один корень многочлена 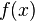— класс смежности элемента .
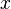Важный пример использования предыдущей конструкции — построение конечных полей. Рассмотрим конечное поле 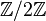из двух элементов и в этом контексте обычно обозначается как 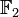. Многочлен 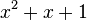неприводим над этим полем (так как не имеет корней), следовательно, факторкольцо 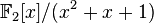является полем. Это поле состоит из четырёх элементов: 0, 1, x и x +1. Все конечные поля можно построить аналогичным образом.

ХАРАКТЕРИСТИКА ПОЛЯ

· Характеристика поля — наименьшее положительное целое 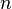число такое, что сумма 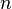копий единицы равна нулю:

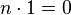
Если такого числа не существует то характеристика равна 0 по определению.

· Характеристика поля всегда 0 или простое число.

Поле характеристики 0 содержит 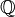, поле рациональных чисел.
Поле характеристики p содержит 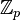, поле вычетов по модулю .

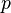ХАРАКТЕРИСТИКА ПОЛЯ

целое положительное простое число или число 0, однозначно определяемое для данного поля следующим образом. Если для нек-рого п>0

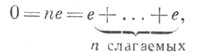
где е - единица поля К, то наименьшее из таких пбудет простым числом и оно наз. характеристикой поля К. Если же такого числа не существует, то говорят, что X. п. Кравна нулю, или что К - поле нулевой характеристики. Иногда такое поле наз. полем без характеристики или полем бесконечной 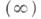характеристики. Всякое поле нулевой характеристики содержит подполе, изоморфное полю всех рациональных чисел, а поле конечной характеристики р - подполе, изоморфное полю классов вычетов по модулю р.