- Группоид — множество с одной бинарной операцией
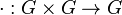 , обычно называемой умножением.
, обычно называемой умножением. - Правая квазигруппа — группоид, в котором возможно правое деление, то есть уравнение
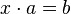 имеет единственное решение для любых
имеет единственное решение для любых 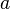 и
и 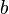 .
. - Квазигруппа — одновременно правая и левая квазигруппы.
- Лупа — квазигруппа с единичным элементом
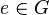 , таким, что
, таким, что 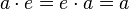 .
. - Полугруппа — группоид, в котором умножение ассоциативно:
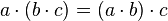 .
. - Моноид — полугруппа с единичным элементом.
- Группа — моноид, в котором для каждого элемента a группы можно определить обратный элемент a −1, такой, что
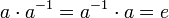 .
. - Абелева группа — группа, в которой операция коммутативна, то есть,
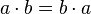 . Операцию в абелевой группе часто называют сложением ('+').
. Операцию в абелевой группе часто называют сложением ('+').
Кольца
- Полукольцо — похоже на кольцо, но без обратимости сложения.
- Почти-кольцо — также обобщение кольца, отличающееся от обычного кольца отсутствием требования коммутативности сложения и отсутствием требования дистрибутивности умножения по сложению (левой или правой)
- Кольцо — структура с двумя бинарными операциями: абелева группа по сложению, моноид по умножению, выполняется закон дистрибутивности:
 .
. - Коммутативное кольцо — кольцо с коммутативным умножением.
- Целостное кольцо — кольцо, в котором произведение двух ненулевых элементов не равно нулю.
- Тело — кольцо, в котором ненулевые элементы образуют группу по умножению.
- Поле — коммутативное кольцо, являющееся телом.
Алгебры
- Алгебра (линейная) — пространство с билинейной дистрибутивной операцией умножения, иначе говоря, кольцо с согласованной структурой пространства
- Ассоциативная алгебра — алгебра с ассоциативным умножением
- Алгебра термов
- Коммутативная алгебра
- Градуированная алгебра
- Алгебра Ли — алгебра с антикоммутативным умножением (обычно обозначаемым
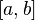 ), удовлетворяющим тождеству Якоби
), удовлетворяющим тождеству Якоби 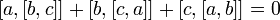
- Алгебра Лейбница — алгебра с умножением (обычно обозначаемым
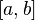 ), удовлетворяющим тождеству Якоби
), удовлетворяющим тождеству Якоби 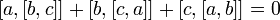
- Алгебра Йордана — коммутативная алгебра с тождеством слабой ассоциативности:
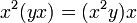
- Алгебра некоммутативная йорданова — некоммутативная алгебра с тождеством слабой ассоциативности:
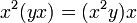 и тождеством эластичности:
и тождеством эластичности: 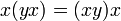
- Альтернативная алгебра — алгебра с тождествами
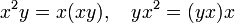
- Алгебра Мальцева — антикоммутативная алгебра с тождеством:
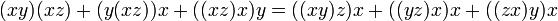
- Коммутантно-ассоциативная алгебра
- Алгебра над операдой — один из наиболее общих видов алгебраических систем. Здесь сама операда играет роль сигнатуры алгебры.
Решётки
- Решётка — структура с двумя коммутативными, ассоциативными, идемпотентными операциями, удовлетворяющими закону поглощения.
- Булева алгебра.
МНОГООБРАЗИЕ
Линейным многообразием в линейном пространстве 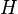 называется подмножество этого пространства вида
называется подмножество этого пространства вида
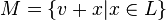
для каких-то фиксированных подпространства 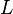 и вектора
и вектора 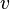 , то есть подмножество, полученное сдвигом каждого элемента из
, то есть подмножество, полученное сдвигом каждого элемента из 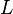 на вектор
на вектор 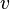 . Обозначение:
. Обозначение:
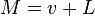
Если 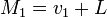 и
и 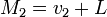 , то
, то 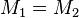 тогда и только тогда, когда и
тогда и только тогда, когда и 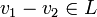 .
.
В частности, 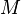 является линейным подпространством тогда и только тогда, когда
является линейным подпространством тогда и только тогда, когда 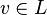 (т.е.
(т.е. 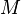 содержит нулевой элемент). В этом случае
содержит нулевой элемент). В этом случае 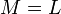 .
.
Если 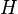 — гильбертово пространство, а
— гильбертово пространство, а 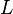 — его замкнутое подпространство, то можно выбрать вектор
— его замкнутое подпространство, то можно выбрать вектор 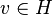 в определении
в определении 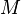 (
(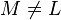 ) ортогональным подпространству
) ортогональным подпространству 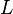 . Такое представление
. Такое представление 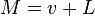 ,
, 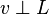 единственно.
единственно.
Пересечение линейных многообразий всегда является линейным многообразием.
Размерность линейного многообразия 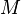 — это размерность линейного подпространства
— это размерность линейного подпространства 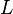 :
: 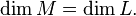 Для линейных многообразий
Для линейных многообразий 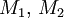 в
в 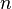 -мерном векторном пространстве или
-мерном векторном пространстве или 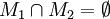 , или
, или 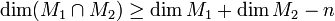
АЛГЕБРАИЧЕСКИХ СИСТЕМ МНОГООБРАЗИЕ
алгебраических систем класс фиксированной сигнатуры и, аксиоматизируемый при помощи тождеств, т. е. формул вида
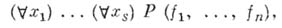
где 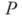 - к.-л. предикатный символ из
- к.-л. предикатный символ из 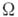 или знак равенства, а
или знак равенства, а  - термы сигнатуры Q от предметных переменных
- термы сигнатуры Q от предметных переменных  А. с. м. наз. иначе э к, вациональными классами, иногда примитивными классами. Многообразие сигнатуры
А. с. м. наз. иначе э к, вациональными классами, иногда примитивными классами. Многообразие сигнатуры 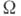 может быть определено также (теорема Биркгофа) как непустой класс
может быть определено также (теорема Биркгофа) как непустой класс 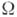 -систем, замкнутый относительно подсистем, гомоморфных образов и декартовых произведений.
-систем, замкнутый относительно подсистем, гомоморфных образов и декартовых произведений.
Пересечение всех многообразий сигнатуры 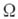 , содержащих данный (не обязательно абстрактный) класс
, содержащих данный (не обязательно абстрактный) класс 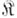
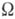 -систем, наз. эквациональным замыканием класса
-систем, наз. эквациональным замыканием класса 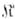 (или многообразием, порожденным классом
(или многообразием, порожденным классом 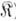 > и обозначается
> и обозначается 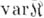 . В частности, если класс
. В частности, если класс 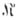 состоит из одной
состоит из одной 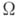 -системы
-системы 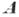 , то его эквацп-ональное замыкание обозначают
, то его эквацп-ональное замыкание обозначают 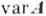 . Если система
. Если система 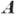 конечна, то все конечно порожденные системы в многообразии
конечна, то все конечно порожденные системы в многообразии 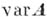 также конечны [1], [2].
также конечны [1], [2].
Пусть 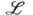 - нек-рый класс
- нек-рый класс 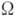 -систем,
-систем, 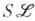 - класс подсистем систем из
- класс подсистем систем из 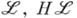 - класс гомоморфных образов систем из
- класс гомоморфных образов систем из 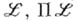 - класс изоморфных копий декартовых произведений систем пз
- класс изоморфных копий декартовых произведений систем пз 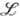 . Для произвольного непустого класса
. Для произвольного непустого класса 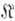
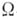 -систем имеет место соотношение (см. [1], [2]):
-систем имеет место соотношение (см. [1], [2]):
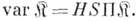
РЕШЁТКА
Решётка (ранее использовался термин структура) — частично упорядоченное множество, в котором каждое двухэлементное подмножество имеет как точную верхнюю (sup), так и точную нижнюю (inf) грани. Отсюда вытекает существование этих граней для любых непустых конечных подмножеств.
Примеры
- множество всех подмножеств данного множества, упорядоченное по включению; например:
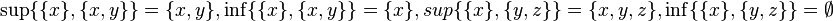 ;
; - всякое линейно упорядоченное множество; причём если
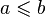 , то
, то 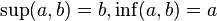 ;
; - множество всех подпространств векторного пространства, упорядоченных по включению, где
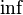 — пересечение, а
— пересечение, а 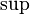 — сумма соответствующих подпространств;
— сумма соответствующих подпространств; - множество всех неотрицательных целых чисел, упорядоченных по делимости:
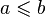 , если
, если 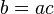 для некоторого
для некоторого  . Здесь
. Здесь 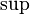 — наименьшее общее кратное, а
— наименьшее общее кратное, а 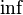 — наибольший общий делитель данных чисел;
— наибольший общий делитель данных чисел; - вещественные функции, определённые на отрезке [0, 1], упорядоченные условием
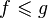 , если
, если 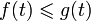 для всех
для всех 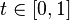 . Здесь
. Здесь
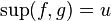 , где
, где 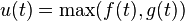 .
.
 2020-08-05
2020-08-05 625
625








