Пусть 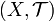 — топологическое пространство и
— топологическое пространство и  — фильтр на множестве
— фильтр на множестве 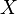 . Точка
. Точка 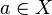 называется пределом фильтра
называется пределом фильтра  , если любая окрестность
, если любая окрестность 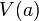 точки
точки 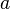 принадлежит фильтру
принадлежит фильтру  . Обозначение:
. Обозначение: 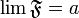 . Для фильтра
. Для фильтра  , порожденного базой
, порожденного базой 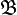 , равенство
, равенство 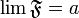 выполняется тогда и только тогда, когда любая окрестность
выполняется тогда и только тогда, когда любая окрестность 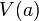 целиком содержит некоторое множество из
целиком содержит некоторое множество из 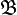 .
.
В хаусдорфовом топологическом пространстве фильтр может иметь не более одного предела.
Точка 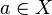 называется предельной точкой (точкой прикосновения, частичным пределом) фильтра
называется предельной точкой (точкой прикосновения, частичным пределом) фильтра  , если
, если 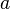 принадлежит замыканию любого множества из
принадлежит замыканию любого множества из  , т.е.
, т.е. 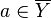 для всех
для всех 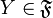 . Равносильно, для любой окрестности
. Равносильно, для любой окрестности 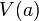 точки
точки 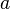 и для любого
и для любого 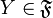 выполнено
выполнено 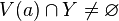 . Любая предельная точка ультрафильтра является его пределом.
. Любая предельная точка ультрафильтра является его пределом.
В компактном топологическом пространстве любой фильтр имеет предельную точку, а любой ультрафильтр имеет предел.
Примеры
- Множество всех окрестностей точки топологического пространства является фильтром;
- Если
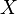 — бесконечное множество, то множество дополнений конечных множеств является фильтром. Такой фильтр называется коконечным фильтром или фильтром Фреше.
— бесконечное множество, то множество дополнений конечных множеств является фильтром. Такой фильтр называется коконечным фильтром или фильтром Фреше. - Если
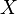 — бесконечное множество мощности
— бесконечное множество мощности 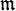 , то множество дополнений множеств мощности
, то множество дополнений множеств мощности 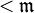 тоже является фильтром.
тоже является фильтром.
УЛЬТРАФИЛЬТР
Ультрафильтр на решётке 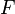 — это максимальный собственный фильтр. Понятие ультрафильтра появилось в общей топологии, где оно используется для обобщения понятия сходимости на пространства с несчётной базой.
— это максимальный собственный фильтр. Понятие ультрафильтра появилось в общей топологии, где оно используется для обобщения понятия сходимости на пространства с несчётной базой.
Определение
Собственный фильтр 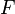 на решётке
на решётке 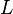 является ультрафильтром, если он не содержится ни в одном собственном (т.е. отличном от
является ультрафильтром, если он не содержится ни в одном собственном (т.е. отличном от 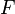 ) фильтре.
) фильтре.
Набор 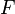 подмножеств множества
подмножеств множества 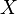 называется ультрафильтром на
называется ультрафильтром на 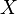 , если
, если
-
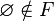
- для любых двух элементов
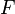 , их пересечение также лежит в
, их пересечение также лежит в 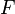
- для любого элемента
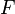 , все его надмножества лежат в
, все его надмножества лежат в 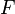
- для любого подмножества
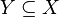 либо
либо 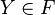 , либо
, либо 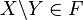
Иначе говоря, если рассмотреть функцию на множествах 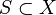 , заданную как
, заданную как 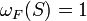 , если
, если 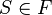 , и
, и 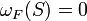 в противном случае, то
в противном случае, то 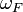 является конечно-аддитивной вероятностной мерой на
является конечно-аддитивной вероятностной мерой на 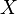 .
.
 2020-08-05
2020-08-05 131
131








