Подмножество 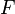 решётки
решётки 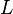 называется фильтром, если
называется фильтром, если
- для всех
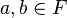 ,
, 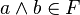
- для всех
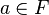 и
и 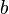 таких, что
таких, что 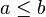 ,
, 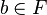
Фильтр называется собственным, если 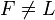 .
.
Собственный фильтр такой, что не существует других собственных фильтров, его содержащих, называется ультрафильтром или максимальным фильтром.
Фильтр 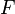 называется простым, если в нём для всех
называется простым, если в нём для всех 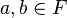 из того, что
из того, что 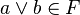 , следует, что либо
, следует, что либо 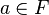 , либо
, либо 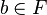 .
.
Минимальный фильтр, содержащий данный элемент 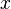 , называется главным фильтром, сгенерированным главным элементом
, называется главным фильтром, сгенерированным главным элементом 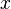 .
.
Если 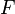 фильтр, то
фильтр, то 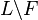 является идеалом.
является идеалом.
Фильтры на множествах
Частным случаем фильтра является фильтр на множестве. Для каждого множества 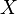 можно определить решётку его подмножеств
можно определить решётку его подмножеств 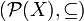 . Тогда фильтр
. Тогда фильтр  на
на 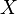 определяется как подмножество
определяется как подмножество 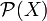 , удовлетворяющее следующим условиям:
, удовлетворяющее следующим условиям:
-
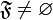
-
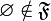
- пересечение любых двух элементов
 лежит в
лежит в 
- надмножество любого элемента
 лежит в
лежит в 
Фильтр вида 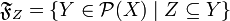 называется фильтром, порожденным множеством
называется фильтром, порожденным множеством 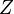 . Фильтр, порожденный множеством из одного элемента, называется главным. Главный фильтр является ультрафильтром.
. Фильтр, порожденный множеством из одного элемента, называется главным. Главный фильтр является ультрафильтром.
База фильтра
Пусть  — фильтр на множестве
— фильтр на множестве 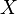 . Семейство подмножеств
. Семейство подмножеств 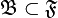 называется базой (базисом) фильтра
называется базой (базисом) фильтра  , если любой элемент фильтра
, если любой элемент фильтра  содержит некоторый элемент базы
содержит некоторый элемент базы 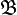 , т.е. для любого
, т.е. для любого 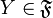 существует
существует 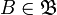 такое, что
такое, что 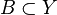 . При этом фильтр
. При этом фильтр  совпадает с семейством всевозможных надмножеств множеств из
совпадает с семейством всевозможных надмножеств множеств из 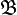 . В частности, фильтры, имеющие общую базу, совпадают. Говорят также, что база
. В частности, фильтры, имеющие общую базу, совпадают. Говорят также, что база 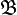 порождает фильтр
порождает фильтр 
Для того, чтобы семейство 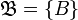 подмножеств множества
подмножеств множества 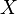 являлось базой некоторого фильтра на
являлось базой некоторого фильтра на 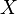 необходимо и достаточно выполнение следующих условий (аксиом базы):
необходимо и достаточно выполнение следующих условий (аксиом базы):
-
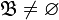 ;
; -
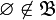 ;
; - для любых
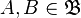 существует
существует 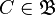 такое, что
такое, что 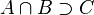 .
.
Две базы 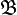 и
и 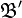 называются эквивалентными, если любой элемент
называются эквивалентными, если любой элемент 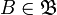 содержит в себе некоторый элемент
содержит в себе некоторый элемент 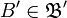 , и наоборот, любой элемент
, и наоборот, любой элемент 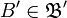 содержит в себе некоторый элемент
содержит в себе некоторый элемент 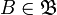 .
.
Эквивалентные базы порождают один и тот же фильтр. Среди всех баз, эквивалентных данной базе 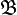 существует максимальная по включению база, а именно, порождаемый этой базой фильтр
существует максимальная по включению база, а именно, порождаемый этой базой фильтр  . Таким образом, между классами эквивалентных баз и фильтрами существует естественное взаимно-однозначное соответствие.
. Таким образом, между классами эквивалентных баз и фильтрами существует естественное взаимно-однозначное соответствие.
Сравнение фильтров
Пусть на множестве 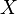 заданы два фильтра
заданы два фильтра  и
и 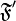 . Говорят, что фильтр
. Говорят, что фильтр 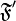 мажорирует фильтр
мажорирует фильтр  (
(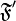 сильнее
сильнее  ,
, 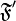 тоньше
тоньше  ), если
), если 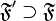 . В этом случае также говорят, что фильтр
. В этом случае также говорят, что фильтр  мажорируется фильтром
мажорируется фильтром 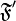 (
( слабее
слабее 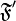 ,
,  грубее
грубее 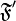 ).
).
Говорят, что база 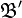 сильнее базы
сильнее базы 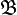 , и записывают
, и записывают 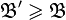 , если любой элемент
, если любой элемент 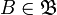 содержит в себе некоторый элемент
содержит в себе некоторый элемент 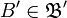 . База
. База 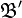 сильнее базы
сильнее базы 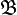 тогда и только тогда, когда фильтр
тогда и только тогда, когда фильтр 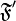 , порожденный базой
, порожденный базой 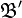 , сильнее фильтра
, сильнее фильтра  , порожденного базой
, порожденного базой 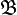 .
.
Базы 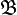 и
и 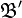 эквивалентны тогда и только тогда, когда одновременно
эквивалентны тогда и только тогда, когда одновременно 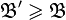 и
и 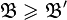 .
.
 2020-08-05
2020-08-05 105
105








