Если решётка 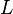 является булевой алгеброй, то возможна следующая характеризация ультрафильтров: фильтр
является булевой алгеброй, то возможна следующая характеризация ультрафильтров: фильтр 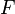 является ультрафильтром тогда и только тогда, когда для любого элемента
является ультрафильтром тогда и только тогда, когда для любого элемента 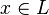 либо
либо 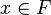 , либо
, либо 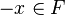
Эта характеризация делает ультрафильтры похожими на полные теории.
Примеры
- любой главный фильтр является ультрафильтром
- подмножество алгебры Линденбаума — Тарского полной теории
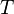 , состоящее из теорем
, состоящее из теорем 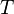
Свойства
- ультрафильтр на конечном множестве всегда является главным.
- любой ультрафильтр на бесконечном множестве содержит конечный фильтр.
- если
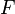 — главный ультрафильтр на множестве
— главный ультрафильтр на множестве 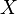 , то его главный элемент является пересечением всех элементов ультрафильтра.
, то его главный элемент является пересечением всех элементов ультрафильтра. - если
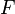 — неглавный ультрафильтр на множестве
— неглавный ультрафильтр на множестве 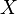 , то пересечение всех его элементов пусто.
, то пересечение всех его элементов пусто.
УЛЬТРАПРОИЗВЕДЕНИЕ
Пусть 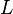 — язык.
— язык. 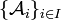 — семейство алгебраических систем,
— семейство алгебраических систем, 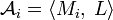 . Прямым произведением алгебраических систем
. Прямым произведением алгебраических систем 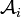 ,
, 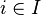 , называется алгебраическая система
, называется алгебраическая система 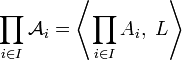 , где для каждого предикатного символа
, где для каждого предикатного символа 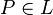
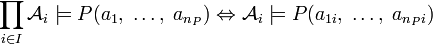 для каждого
для каждого 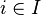 ;
;
для каждого функционального символа 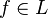
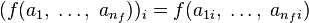
и для каждого константного символа 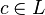
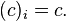
Пусть 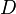 — фильтр над
— фильтр над 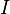 . Определим на
. Определим на 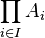 отношение
отношение 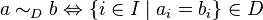 . Введём обозначения:
. Введём обозначения:
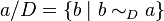 ,
, 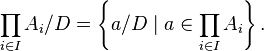
Определим алгебраическую систему 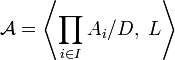 следующим образом.
следующим образом.
Положим для предикатного символа 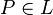
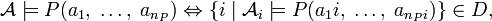
для каждого функционального символа 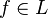
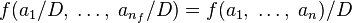
и для константных символов 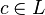
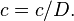
Определённая таким образом алгебраическая система 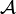 называется фильтрованным произведением систем
называется фильтрованным произведением систем 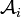 по фильтру
по фильтру 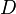 и обозначается
и обозначается 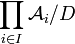 . Если
. Если 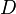 — ультрафильтр, то
— ультрафильтр, то 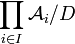 называется ультрапроизведением, если все
называется ультрапроизведением, если все 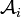 совпадают и равны
совпадают и равны 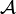 , то
, то 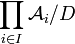 называется ультрастепенью
называется ультрастепенью 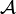 и обозначается
и обозначается 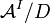 .
.
Основное свойство ультрапроизведений состоит в том, что они сохраняют все предложения:
Теорема Лося. Пусть 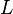 — язык,
— язык, 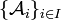 — семейство алгебраических систем языка
— семейство алгебраических систем языка 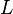 ,
, 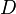 — ультрафильтр над
— ультрафильтр над 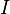 . Тогда для любой формулы
. Тогда для любой формулы 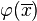 языка
языка 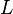 и любой последовательности
и любой последовательности 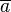 элементов из
элементов из 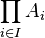
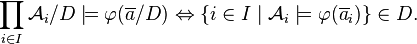
Также теорему компактности можно сформулировать следующим образом.
Теорема компактности. Если множество формул локально выполнимо в некотором классе 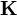 , то оно выполнимо в некотором ультрапроизведении систем из
, то оно выполнимо в некотором ультрапроизведении систем из 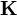
 2020-08-05
2020-08-05 136
136







