Виды сплайнов (интерполяция)

Все сплайны строятся по полиному третьей степени в виде

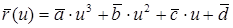                                           (1)

Цель – по известным радиус-векторам получить коэффициенты a, b, c и d интерполяционного полинома (1)

Фюргюссон - Эрмит

Заданы два радиус-вектора 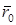 и 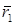 (координаты точек) и 2 радиус-вектора  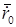и  производных.

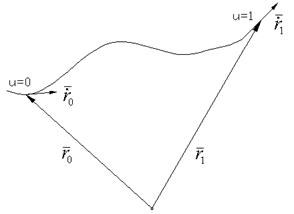
Проецируем 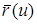 на оси x, y и z ПДСК.

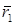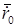; соответственно для ,  и .

Рассмотрим для оси х:

.

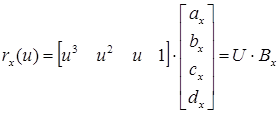Граничные условия

При u = 0 ,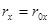

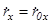
При u = 1 ,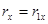

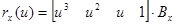
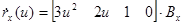
Соответственно имеем

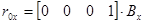
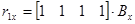
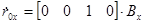
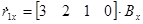
Получаем обратную матрицу

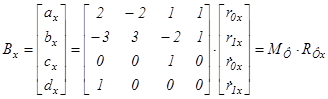
Аналогично для осей у и z

, .

Складывая, замечаем что

Получим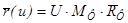

Таким образом, окончательно имеем

(1’)

В скобках – весовые функции.

Рассмотрим две соседние кривые. Условия , .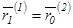

 

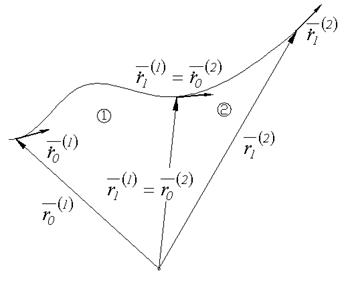
Для исключения перегибов в точке сопряжения кривых 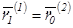. Берем производные уравнения (1)

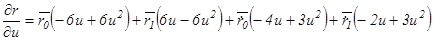
Запишем равенство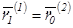

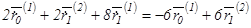
Пример: На концах крайних кривых неизвестны .

Недостатки:

Вычисление дополнительных касательных векторов

Глобальная корректировка

Необходимо знать касательные векторы на концах

Безье – Бернштейн

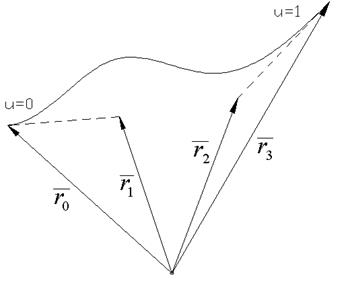
Особенности построения сплайна

Определяется четырьмя точками

Определяются производные

;

;

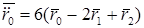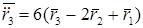
В общем виде

;

;

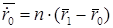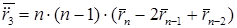
 или иначе

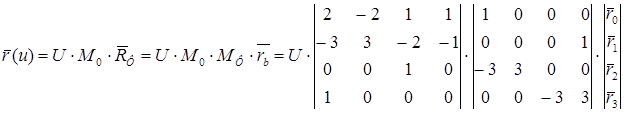
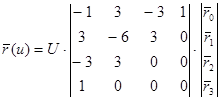
Окончательно имеем

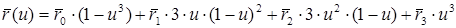
Графики весовых (базисных) функций

Заметим, что функции симметричны. В 1912 году Берштейн вывел полиномы, а Безье их модифицировал.

,

i = 0…n, n – количество точек, i – номер текущей точки

Недостатки:

Глобальная корректировка

Степень полинома определяется количеством точек

Аппарат Безье применяется для поверхностей класса А – скульптурные, поверхности автомобилей.