VII. Различные случаи сложения и вычитания рациональных чисел

Рассмотрим примеры сложения и вычитания рацио­нальных чисел, когда слагаемые представляют собой не только обыкновенные дроби, но и целые числа, десятичные дроби или смешанные числа.

Пример 1.

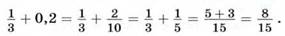
Выполняя сложение обыкновенной дроби и деся­тичной, мы перевели десятичную дробь в обыкно­венную.

Иногда можно перевести обыкновенную дробь в десятичную (если при этом получается конечная десятичная дробь). Например:

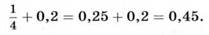
Пример 2.

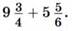
Сложение смешанных чисел можно выполнить разными способами.

Например, переведём смешанные числа в непра­вильные дроби:

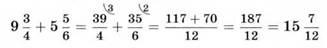
Выполним сложение другим способом, используя то, что смешанное число можно представить в виде суммы целой и дробной частей:

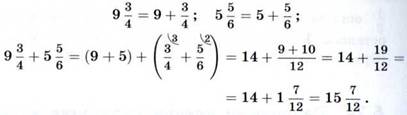
То же самое можно записать короче:

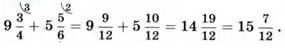
Пример 3.

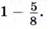
Обыкновенная дробь вычитается из еди­ницы.

Раздробим единицу на нужные доли — пред­ставим единицу в виде неправильной дроби со знаменателем 8:

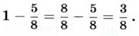
При этом говорят, что найдено дополнение дроби до единицы.

Пример 4. Рассмотрим, в чем особенности вычитания смешанных чисел.

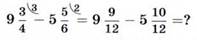
Мы столкнулись с проблемой — дробная часть уменьшаемого меньше, чем дробная часть вычитаемого. Выйти из затруднительной ситуации можно разными способами. Например:

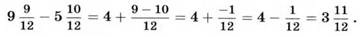
Или так:

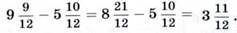
Во втором случае мы «заняли» в целой части уменьшаемого единицу, раздробив её на нужные доли.

Рассмотрим несколько примеров сложения раци­ональных чисел с одинаковыми и разными знака­ми. Не забывайте, что в числовых выражениях, в которых содержатся только действия сложения и вычитания, знаки «+» и «—» можно считать не знаками действий, а знаками слагаемых.

Пример 5.

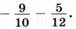
Складываются числа с одинаковыми знаками.

Можно поступить так: поставить общий знак и сложить модули чисел:

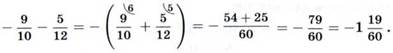
Или так (знак каждого слагаемого считать относя­щимся к числителю дроби):

Пример 6.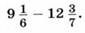

Складываются числа с разными: знаками.

Можно поступить так: выбрать слагаемое с боль­шим модулем, поставить знак этого числа у всего выражения и вычесть из большего модуля мень­ший:

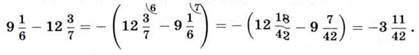
Или так:

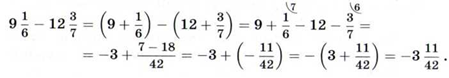
Таким образом:

1. Чтобы сложить смешанные числа, можно сложить их целые части и приписать к результату сумму дробных частей.

2. При сложении двух отрицательных рациональных чисел можно действовать по общему правилу: поставить общий знак «—» и сложить модули чисел.

3. При сложении двух рациональных чисел с разными знаками можно действовать по общему правилу: выбрать слагаемое с большим модулем, поставить знак этого числа перед всем выражением и вычесть из большего модуля меньший.

4. При сложении или вычитании рациональных чисел, содержащих целые и дробные части, можно:

• записать каждое число в виде суммы целой и дробной частей;

• в полученном числовом выражении раскрыть скобки;

• сложить отдельно целые и дробные части;

• найти сумму полученных результатов.