2020-08-05
98
Методы решения геометрических задач средствами линейной алгебры
Методические указания
к решению задач
Санкт-Петербург
Издательство СПбГЭТУ «ЛЭТИ»
2011
МИНОБРНАУКИ РОССИИ
––––––––––––––––––––––––––––––––––––––––
Санкт-Петербургский государственный
электротехнический университет «ЛЭТИ»
––––––––––––––––––––––––––––––––––––––––
Методы решения геометрических задач средствами линейной алгебры
Методические указания
к решению задач
Санкт-Петербург
Издательство СПбГЭТУ «ЛЭТИ»
2011
УДК 514.12
Методы решения геометрических задач средствами линейной алгебры: Методические указания к решению задач / Сост.: М. В. Буслаева, Л. А. Бровкина, А. С. Колпаков, В. А. Смирнова. СПб.: Изд-во СПбГЭТУ «ЛЭТИ», 2011. 32 с.
Содержат простейшие формулы и примеры решения задач различными способами по теме «Плоскость и прямая в пространстве».
Предназначены для студентов первого курса дневной формы обучения.
Утверждено
редакционно-издательским советом университета
в качестве методических указаний
Редактор Н. В. Лукина
–––––––––––––––––––––––––––––––––––––––––––––––
Подписано в печать..11. Формат 60´84 1/16.
Бумага офсетная. Печать офсетная. Печ. л. 2.0.
Гарнитура «Times New Roman». Тираж 110 экз. Заказ .
–––––––––––––––––––––––––––––––––––––––––––––––––
Издательство СПбГЭТУ «ЛЭТИ»
197376, С.-Петербург, ул. Проф. Попова, 5
© СПбГЭТУ «ЛЭТИ», 2011
Цель настоящих методических указаний заключается в том, чтобы представить набор типовых задач по следующим разделам аналитической геометрии: «Плоскость», «Прямая в пространстве», «Плоскость и прямая». Предложенный набор упражнений ориентирован на освоение ключевых теоретических понятий и утверждений посредством приобретения практических навыков решения стандартных задач по курсу. При этом не требуется применения каких-либо нетрадиционных приемов или теоретических утверждений, выходящих за рамки курса.
ПЛОСКОСТЬ
Основные сведения из теории
В декартовой системе координат 
плоскость 
может быть задана уравнением одного из следующих видов.
1. Общее уравнение плоскости:
Вектор 
перпендикулярен плоскости.
2. Уравнение плоскости, проходящей через заданную точку 
перпендикулярно нормальному вектору , имеет вид
(1.2)
3. Уравнение плоскости в отрезках на осях:
(1.3)
Здесь 
величины направленных отрезков, отсекаемых плоскостью на координатных осях 
соответственно, т. е. плоскость проходит через три точки: 
, 
, 
.
Кроме того, понадобятся следующие формулы, доказательство которых можно найти в теоретическом курсе. 
4. Угол 
между двумя плоскостями
и
равен углу между нормальными векторами 
и 
:
; 
(1.4)
Плоскости 
и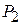 
параллельны тогда и только тогда, когда векторы 
и 
коллинеарны (
):
.
Плоскости и 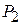перпендикулярны тогда и только тогда, когда векторы и 
ортогональны (
):
5. Расстояние от точки 
до плоскости : 
равно
(1.5)
6. Уравнение плоскости, проходящей через линию пересечения двух плоскостей
и
,
следует искать в виде
, (1.6)
где 
и 
некоторые числа.
Множество плоскостей, проходящих через линию пересечения двух заданных плоскостей, называется пучком плоскостей.
