Плоскость и прямая в пространстве

Основные сведения из теории

Пусть прямая задана каноническими уравнениями

: ,

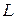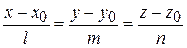 а плоскость – общим уравнением

: .

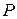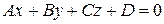1. Угол между прямой и плоскостью равен углу между направляющим вектором 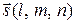 прямой и нормальным вектором  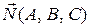плоскости и вычисляется по формуле

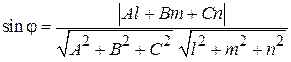.                      (3.1)

2. Условие параллельности прямой и плоскости имеет вид

.

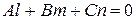Оно равносильно условию ортогональности векторов 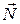 и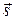

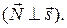
3. Условие перпендикулярности прямой и плоскости имеет вид

.

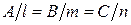Оно равносильно условию коллинеарности векторов 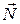 и .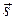

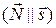4. Условие принадлежности прямой 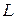 плоскости  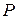записывается в виде

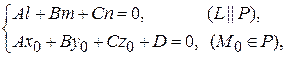                            (3.2)

где 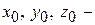 координаты точки 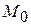, принадлежащей прямой.