Задача 2.1. Найти канонические уравнения прямой, заданной как линия пересечения двух плоскостей: 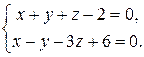
Решение. Прямая задана общими уравнениями (2.1). Найдем какую-нибудь точку 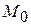 на прямой. Выберем, например,
на прямой. Выберем, например, 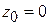 . Другие координаты получим из системы уравнений
. Другие координаты получим из системы уравнений 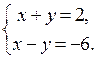 Очевидно, что
Очевидно, что 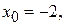
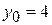 . Следовательно,
. Следовательно, 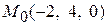 . Затем находим направляющий вектор
. Затем находим направляющий вектор 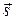 прямой. Так как прямая принадлежит одновременно обеим плоскостям, то вектор
прямой. Так как прямая принадлежит одновременно обеим плоскостям, то вектор 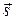 ортогонален нормальным векторам этих плоскостей, т. е.
ортогонален нормальным векторам этих плоскостей, т. е. 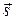
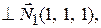
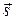
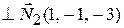 (рис. 2.1). Поэтому за направляющий вектор
(рис. 2.1). Поэтому за направляющий вектор 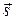 можно принять
можно принять
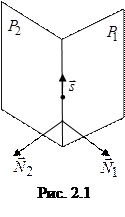
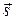
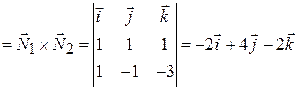 .
.
Подставляя координаты направляющего вектора 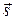 и точки
и точки 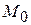 в уравнения прямой (2.3), получим
в уравнения прямой (2.3), получим
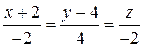
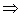
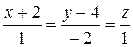 .
.
Ответ: 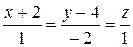 .
.
 Полезная формула. Если прямая задана как линия пересечения двух плоскостей:
Полезная формула. Если прямая задана как линия пересечения двух плоскостей:
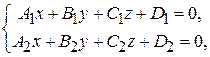
то ее направляющий вектор 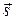 можно выбрать в виде
можно выбрать в виде
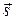
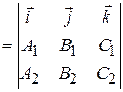 . (2.6)
. (2.6)
Задача 2.2. Найти параметрические и канонические уравнения прямой, проходящей через точку 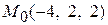 и параллельной вектору
и параллельной вектору 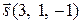 .
.
Решение. Известны точка 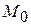 и направляющий вектор
и направляющий вектор 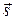 прямой.
прямой.
Согласно формуле (2.2) параметрические уравнения прямой имеют вид
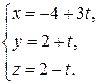
Канонические уравнения получаем, используя формулу (2.3):
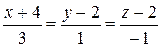 .
.
Ответ: 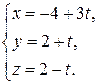
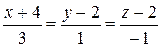 .
.
Задача 2.3. Найти направляющий вектор прямой 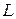 :
: 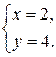
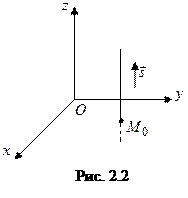 Решение. Прямая
Решение. Прямая 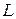 проходит через точку
проходит через точку 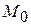 (2, 4) на плоскости
(2, 4) на плоскости 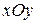 и параллельна оси
и параллельна оси 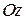 (рис. 2.2). Очевидно, что ее направляющий вектор можно выбрать в виде
(рис. 2.2). Очевидно, что ее направляющий вектор можно выбрать в виде 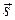 (0, 0, 1).
(0, 0, 1).
Ответ: 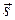 (0, 0, 1).
(0, 0, 1).
Задача 2.4. Найти косинусы углов, которые образует с осями координат прямая
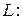
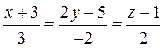 .
.
Решение. Обозначим через 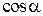 ,
, 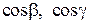 косинусы углов прямой
косинусы углов прямой 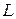 с осями
с осями 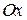 ,
, 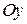 и
и 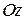 соответственно. Они, очевидно, равны направляющим косинусам вектора
соответственно. Они, очевидно, равны направляющим косинусам вектора 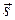 прямой. Из уравнений прямой находим
прямой. Из уравнений прямой находим 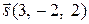 .
.
Следовательно,
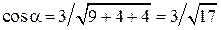 ;
; 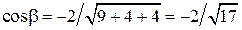 ;
; 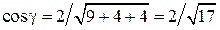 .
.
(Напомним, что 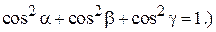
Ответ: 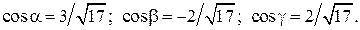
Задача 2.5. Найти косинус острого угла между прямыми
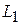 :
: 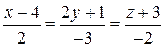 ;
; 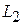 :
: 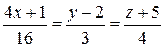 .
.
Решение. Из уравнений прямых вытекает, что направляющий вектор прямой 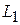 равен
равен 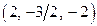 , направляющий вектор прямой
, направляющий вектор прямой 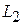 равен
равен 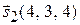 . Для удобства вычислений направляющий вектор прямой
. Для удобства вычислений направляющий вектор прямой 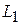 выберем в виде
выберем в виде 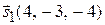 . Он коллинеарен исходному. Используя формулу (2.5), получаем
. Он коллинеарен исходному. Используя формулу (2.5), получаем 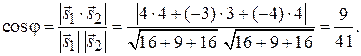
Ответ: 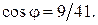
Задача 2.6. Показать, что прямая 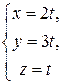 перпендикулярна прямой
перпендикулярна прямой
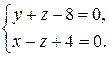
Решение. Направляющий вектор первой прямой, очевидно, равен 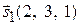 , направляющий вектор второй прямой
, направляющий вектор второй прямой 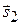 найдем с помощью формулы (2.6):
найдем с помощью формулы (2.6):
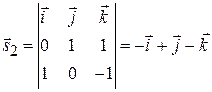 .
.
Вычислим скалярное произведение векторов 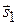 и
и 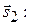
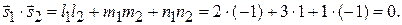
Ответ: прямые перпендикулярны.
Задача 2.7. Проверить, лежат ли три данные точки 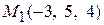 ,
, 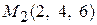 и
и 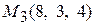 на одной прямой.
на одной прямой.
Решение. Напишем уравнения прямой, проходящей через две заданные точки 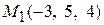 и
и 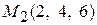 , согласно формуле (2.4). Получим
, согласно формуле (2.4). Получим
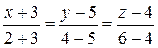
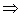
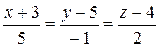 .
.
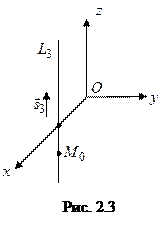 Проверим, удовлетворяют ли координаты точки
Проверим, удовлетворяют ли координаты точки 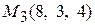 этим уравнениям. После подстановки
этим уравнениям. После подстановки 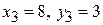 получаем:
получаем: 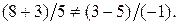 Следовательно, точка
Следовательно, точка 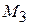 не лежит на прямой.
не лежит на прямой.
Ответ: не лежат.
Задача 2.8. Найти канонические уравнения прямых 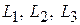 , проходящих через точку
, проходящих через точку 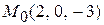 параллельно: 1) оси
параллельно: 1) оси 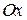 ; 2) оси
; 2) оси 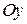 ; 3) оси
; 3) оси 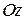 .
.
Решение. Найдем уравнения прямой 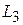 , проходящей через точку
, проходящей через точку 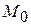 параллельно оси
параллельно оси 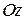 . Ее направляющий вектор
. Ее направляющий вектор 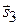 можно выбрать в виде
можно выбрать в виде 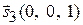 (рис. 2.3).
(рис. 2.3).
Используя формулу (2.3), получим
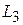 :
: 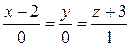 .
.
Таким же образом находим 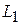 и
и 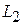 .
.
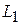 :
: 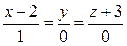 ,
, 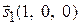 ;
;
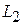 :
: 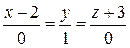 ,
, 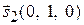 .
.
Ответ: 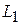 :
: 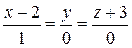 ;
; 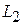 :
: 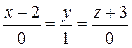 ;
; 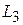 :
: 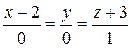 .
.
Задача 2.9. Найти точки пересечения прямой 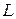 :
: 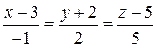 с плоскостями координат.
с плоскостями координат.
Решение. Для того чтобы найти точку пересечения прямой 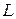 с плоскостью
с плоскостью 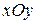 , в канонических уравнениях прямой
, в канонических уравнениях прямой 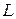 следует положить
следует положить 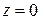 . Получим
. Получим 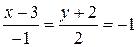 , откуда
, откуда 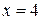 ,
, 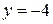 . Таким образом, прямая
. Таким образом, прямая 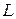 пересекает плоскость
пересекает плоскость 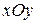 в точке
в точке 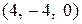 . Аналогично находим точки пересечения с плоскостями
. Аналогично находим точки пересечения с плоскостями 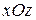 и
и 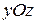 .
.
Ответ: 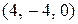 ;
; 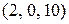 ;
; 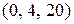 .
.
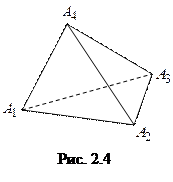 Задача 2.10. Известны координаты вершин тетраэдра:
Задача 2.10. Известны координаты вершин тетраэдра: 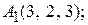
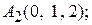
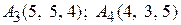 . Составить канонические уравнения его ребер и найти их длины.
. Составить канонические уравнения его ребер и найти их длины.
Решение. Условие такое же, как и в задаче 1.10 (рис. 2.4). Найдем уравнения ребра 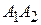 . Для этого подставим координаты вершин
. Для этого подставим координаты вершин 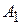 и
и 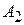 в формулу (2.4). Получим
в формулу (2.4). Получим 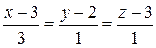 . Теперь можно определить длину ребра
. Теперь можно определить длину ребра 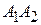 :
:
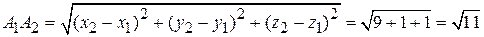 .
.
Уравнения и длины остальных ребер найдите самостоятельно.
Ответ: 1) 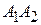 :
: 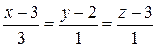 ,
, 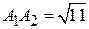 ;
;
2) 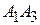 :
: 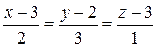 ,
, 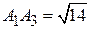 ;
;
3) 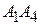 :
: 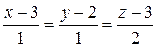 ,
, 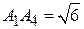 ;
;
4) 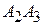 :
: 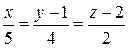 ,
, 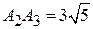 ;
;
5) 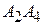 :
: 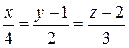 ,
, 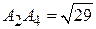 ;
;
6) 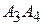 :
: 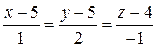 ,
, 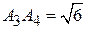 .
.
Задача 2.11. Найти точку пересечения двух прямых
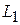 :
: 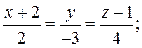
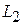 :
: 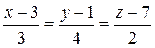 .
.
Решение. Перепишем уравнения прямых в параметрическом виде
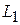 :
: 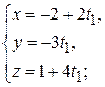
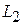 :
: 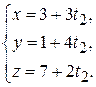
Для нахождения точки пересечения этих прямых нужно решить систему уравнений:
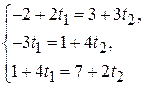
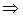
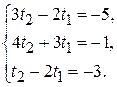
Очевидно, она имеет единственное решение 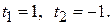 Подставляя значение параметра
Подставляя значение параметра 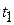 в параметрические уравнения прямой
в параметрические уравнения прямой 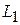 (или
(или 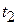 в уравнения прямой
в уравнения прямой 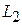 ), получим
), получим 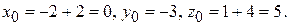
Ответ: 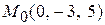 .
.
Задача 2.12. Найти биссектрису 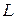 острого угла между прямыми
острого угла между прямыми
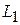 :
: 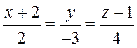 ;
; 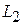 :
: 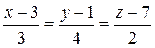 .
.
Решение. Точка пересечения этих прямых 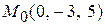 найдена в ходе решения задачи 2.11. Убедимся теперь, что направляющие векторы
найдена в ходе решения задачи 2.11. Убедимся теперь, что направляющие векторы 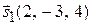 и
и 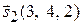 прямых
прямых 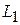 и
и 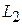 образуют острый угол. Действительно,
образуют острый угол. Действительно,
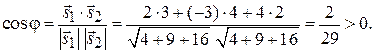
Очевидно, что 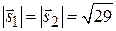 . (Направляющие векторы
. (Направляющие векторы 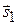 и
и 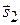 всегда можно взять равными по длине, например единичными.) Так как
всегда можно взять равными по длине, например единичными.) Так как 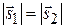 , то параллелограмм, построенный на векторах
, то параллелограмм, построенный на векторах 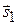 и
и 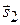 как на сторонах, является ромбом, а диагональ
как на сторонах, является ромбом, а диагональ 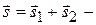 биссектрисой его угла. Следовательно, вектор
биссектрисой его угла. Следовательно, вектор 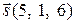 может быть выбран в качестве направляющего вектора биссектрисы
может быть выбран в качестве направляющего вектора биссектрисы 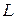 .
.
Таким образом, известно, что искомая прямая проходит через точку 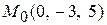 и ее направляющий вектор равен
и ее направляющий вектор равен 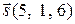 . Запишем канонические уравнения
. Запишем канонические уравнения 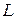 согласно формуле (2.3):
согласно формуле (2.3):
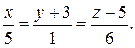
Чертеж к этой задаче предлагаем сделать самостоятельно.
Ответ: 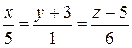 .
.
 2020-08-05
2020-08-05 112
112








