Основные сведения из теории
Прямая 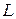 в пространстве может быть задана уравнением одного из следующих видов.
в пространстве может быть задана уравнением одного из следующих видов.
1. Общие уравнения прямой:
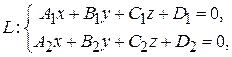 (2.1)
(2.1)
где коэффициенты 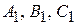 не пропорциональны коэффициентам
не пропорциональны коэффициентам 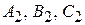 . Это равносильно заданию прямой как линии пересечения двух плоскостей.
. Это равносильно заданию прямой как линии пересечения двух плоскостей.
2. Параметрические уравнения прямой:
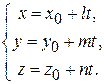 (2.2)
(2.2)
Здесь 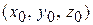 – координаты какой-либо точки
– координаты какой-либо точки 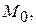 принадлежащей прямой
принадлежащей прямой 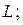
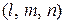 – координаты вектора
– координаты вектора 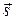 , параллельного прямой. Вектор
, параллельного прямой. Вектор 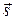 называется направляющим вектором прямой. Переменная
называется направляющим вектором прямой. Переменная 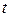 – параметр,
– параметр, 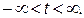
3. Канонические уравнения прямой:
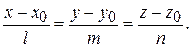 (2.3)
(2.3)
4. Уравнения прямой, проходящей через две заданные точки 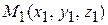 и
и 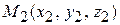 :
:
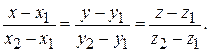 (2.4)
(2.4)
Кроме того, при решении задач будут использоваться следующие формулы, доказательство которых можно найти в теоретическом курсе.
5. Угол 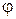 между двумя прямыми
между двумя прямыми
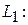
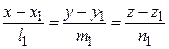 ;
; 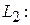
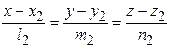
равен углу между направляющими векторами 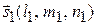 и
и 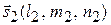 :
:
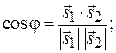
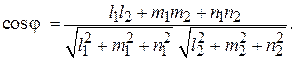 (2.5)
(2.5)
Прямые 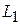 и
и 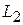 параллельны тогда и только тогда, когда векторы
параллельны тогда и только тогда, когда векторы 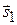 и
и 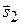 коллинеарны (
коллинеарны (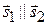 ):
):
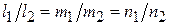 .
.
Прямые 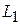 и
и 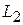 перпендикулярны тогда и только тогда, когда векторы
перпендикулярны тогда и только тогда, когда векторы 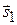 и
и 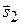 ортогональны (
ортогональны (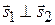 ):
):
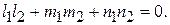
 2020-08-05
2020-08-05 87
87








