Принцип наименьшего действия (принцип Гамильтона). Уравнения Лагранжа

       Самая общая формулировка закона движения системы с  степенями свободы дается принципом наименьшего действия (или принципом Гамильтона). Согласно этому принципу, каждая механическая система полностью характеризуется своей функцией Лагранжа. Функция Лагранжа зависит от обобщенных координат 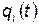, обобщенных скоростей  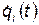и времени :

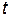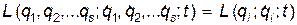
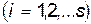                                  (1)

Для сокращения записи обычно пишут:

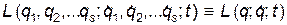                            (2)

Пусть в начальный и конечный моменты времен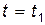и  и 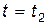, положение всех точек системы характеризуются двумя наборами значений обобщенных координат:  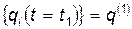   и 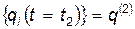; 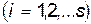. Тогда интеграл по времени

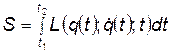                                             (3)

называется действием для данной механической системы.

Принцип наименьшего действия формулируется следующим образом: пусть известна функция Лагранжа 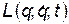 для данной системы. Тогда, между начальным  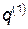и конечным 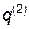положениями, система будет двигаться таким образом, чтобы интеграл действия имел наименьшее значение:

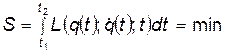                               (4)

только те функции 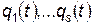, которые удовлетворяют условию минимума действия и будут являться истинными "траекториями" движения. Из условия (4) можно получить уравнения для истинных траекторий движения всех точек между начальным и конечным положением системы. Эти уравнения называются уравнениями Лагранжа.

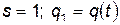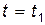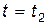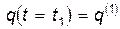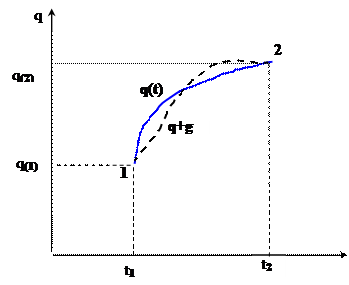
Получим эти уравнения. Для простоты рассмотрим систему с одной степенью свободы: . Пусть в моменты времени  и  система находилась в заданных положениях  и 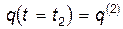. Рассмотрим траекторию 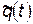, «близкую» к  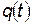и проходящую через те же самые точк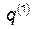и  и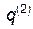

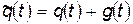
Функция 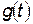 является «малой» добавкой к 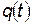: 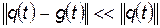. Понятно, что для начального и для конечного положения системы  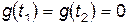(см. рисунок). Тогда, для новой обобщенной скорости  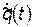будем иметь

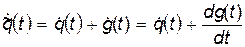
Условие экстремальности действия определяется равенством нулю его вариации:

                             (5)

Это условие есть обобщение хорошо известного признака экстремальности функции 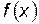: в тех точках, где функция  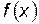имеет минимум или максимум, её производная 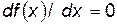. Следовательно, равен нулю и её дифференциал: 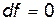. Формула (5) фактически обобщает признак экстремальности функции для функционала, которым и является интеграл действия.

Вычислим эту вариацию 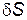. Учитывая, что при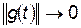

,

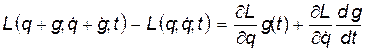запишем

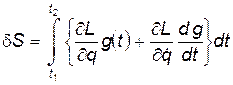
Проинтегрируем второе слагаемое по частям и учтем, что :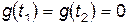

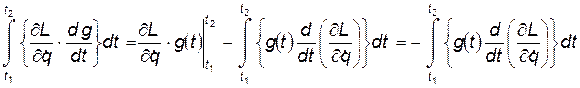
Теперь условие экстремальности действия запишется так:

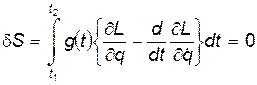                        (6)

Поскольку функция 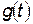 - произвольная, то условие (6) может быть удовлетворено только в случае - когда выражение в его фигурных скобках обращается в ноль:

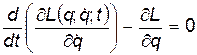                           (7)

Это и есть уравнение Лагранжа. для мех. системы с одной степенью свободы. Конкретный вид уравнения (7) зависит от конкретного вида ф. Лагранжа. О том, что собой представляет ф. Лагранжа речь пойдет ниже.

Поскольку уравнение Лагранжа (7) является дифференциальным уравнением второго порядка, его общее решение зависит от двух произвольных констант: 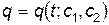. Чтобы определить эти константы необходимо задать два начальных условия:  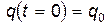и 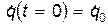. Таким образом, для определения закона движения системы с одной степенью свободы необходимо решить задачу Коши:

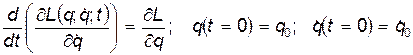(8)

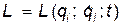
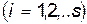Если система имеет  степеней свободы ( ), то вариацию действия нужно осуществлять независимо по каждой обобщенной координате 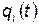. В результате получим систему однотипных  уравнений с 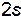 начальными условиями:

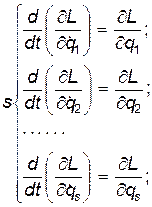
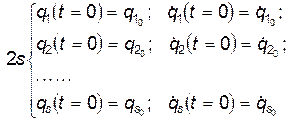     (9)

В компактном виде систему уравнений и начальных условий (9) обычно записывают так:

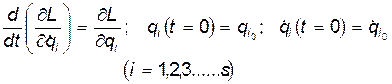  (10)

Основные свойства функции Лагранжа:

1. Функцию Лагранжа можно умножить на любое число. Уравнения Лагранжа (10) при этом не изменяются.

2. Функция Лагранжа обладает важным свойством аддитивности.

Пусть система АВ состоит из двух подсистем: А и В. Её Функция Лагранжа 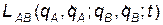 будет зависеть от обобщенных координат и скоростей всех частиц подсистемы А, т.е. от 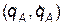, и всех частиц подсистемы В, т.е. от 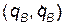. Предположим теперь, что подсистемы А и В начнут удаляться друг от друга на очень большое расстояние:  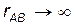(см. рисунок).

Понятно, что в этом случае движение точек в подсистемах А и В будет происходить независимо и никак не влиять друг на друга. Но это означает, что уравнения Лагранжа для системы АВ должны распасться на две независимые системы уравнений для подсистем А и В, соответственно:

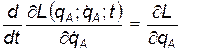и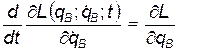

Для этого необходимо, чтобы

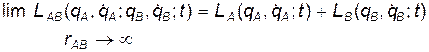     (11)

3. Функция Лагранжа любой мех. системы определена неоднозначно, а с точностью до полной производной по времени от произвольной функции координат и времени.

Действительно, пусть 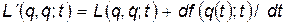, где 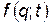 - произвольная функция. Запишем действие , используя ф. Лагранжа :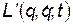

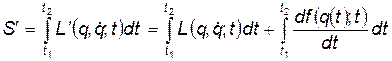
Следовательно

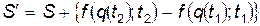
Величина, стоящая в фигурных скобках, есть некоторое число, которое исчезает при вариации действия. Поэтому 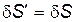 при любом виде функции 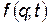, а уравнения Лагранжа будут иметь один и тот же вид независимо от того, какую функцию Лагранжа  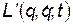или 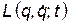 мы выбираем.