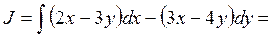 (*)
(*)
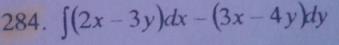

РЕШЕНИЕ:
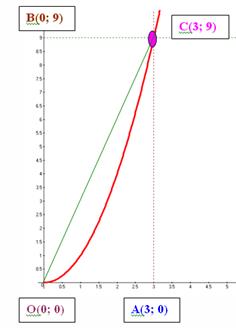
Построим линию, по которой надо вести интегрирование:
1) L − отрезок прямой ОС
Записываем уравнение прямой ОС как уравнение прямой, проходящей через точки О и С:
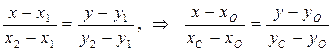
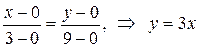

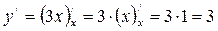
Воспользуемся формулой

Находим:

2) L − дуга параболы 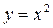

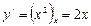
Воспользуемся формулой
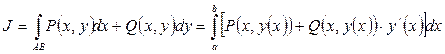
Находим:
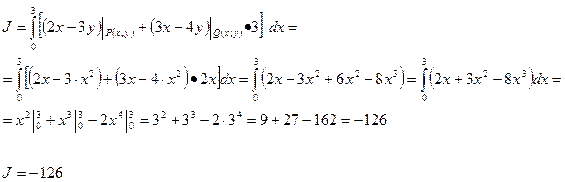
3) L − ломаная ОАС
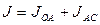
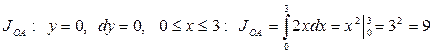


3) L − ломаная ОВС
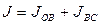
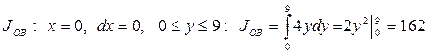

ПРОВЕРКА: 3) и 4) – одинаковый результат: J=90, т.к. криволинейный интеграл здесь не зависит здесь от пути интегрирования: 
Задача № 304. Найти общее решение дифференциального уравнение первого порядка
 (*)
(*) 
РЕШЕНИЕ:
Решаем однородное уравнение: 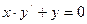
Разделяем переменные и интегрируем:
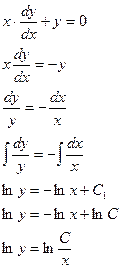
Потенцируем:
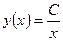
Варьируем С: С=С(х): 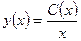 (**)
(**)
Тогда 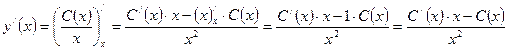
Подставим  и
и  в исходное уравнение и найдем С(х):
в исходное уравнение и найдем С(х):
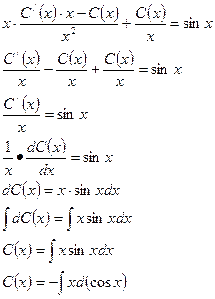
Интегрируем по частям:
Положим 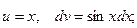 тогда
тогда 
Применяя формулу интегрирования по частям, находим:

Таким образом, общее решение исходного уравнения (*) имеет вид (**):
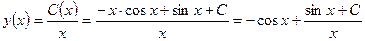
ПРОВЕРКА:
 (*)
(*)

 (*)
(*)
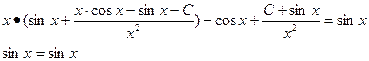
ОТВЕТ:
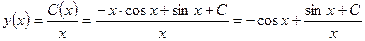
 2020-08-05
2020-08-05 99
99








