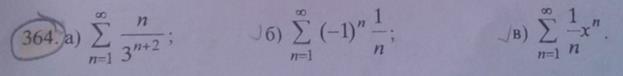
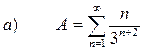
РЕШЕНИЕ:
Исследуем ряд по необходимому признаку:
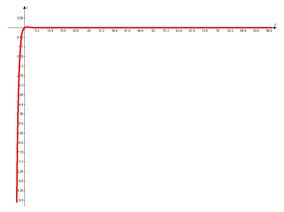
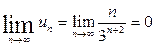
Посмотрим поведение функции 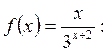
Или используем разложение в ряд:
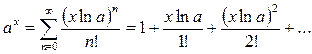
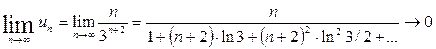
Общий член Un стремится к нулю при 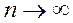 значит, по необходимому признакуисходный ряд сходится.
значит, по необходимому признакуисходный ряд сходится.
Необходимый признак выполняется. Необходимо продолжить исследование по достаточным признакам.
Так как функция 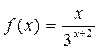 при х ≥ 1 является непрерывной, положительной и монотонно убывающей, то можем воспользоваться интегральным признаком Коши:
при х ≥ 1 является непрерывной, положительной и монотонно убывающей, то можем воспользоваться интегральным признаком Коши: 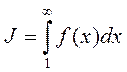 . Находим:
. Находим:

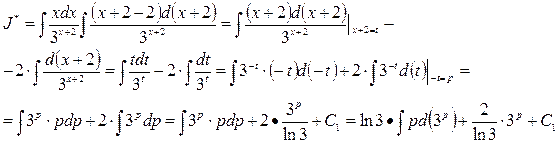
Используем интегрирование по частям:
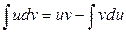
Положим 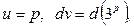 тогда
тогда 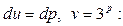
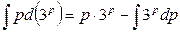
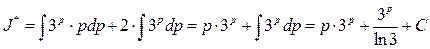
Несобственный интеграл расходится, а, следовательно, вместе с ним расходится исходный ряд.
ОТВЕТ: Ряд расходится
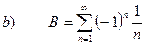
РЕШЕНИЕ:
Имеем знакочередующийся ряд. Воспользуемся признаками Лейбница сходимости знакочередующегося ряда.
1) Очевидно, что по необходимый признак 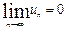 выполняется для данного ряда:
выполняется для данного ряда: 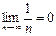
2) 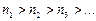 Выполняется.
Выполняется.
Рассмотрим ряд, составленный из абсолютных членов исходного ряда:
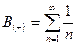
Имеем гармонический ряд, который расходится.
Действительно, так как функция 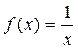 при х ≥ 1 является непрерывной, положительной и монотонно убывающей, то можем воспользоваться интегральным признаком Коши:
при х ≥ 1 является непрерывной, положительной и монотонно убывающей, то можем воспользоваться интегральным признаком Коши: 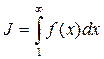 . Находим:
. Находим:
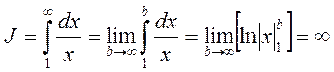
Несобственный интеграл J расходится и, следовательно, вместе с ним расходится ряд В(+).
ОТВЕТ: Ряд сходится условно
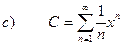
РЕШЕНИЕ:
Для определения области сходимости функционального ряда используем признак Даламбера числового ряда, при этом предел вычисляется от выражений функционального ряда взятых по модулю: 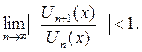
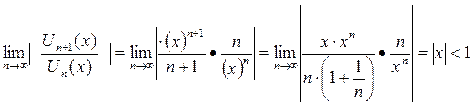
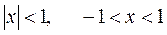
Исследуем ряд на концах найденного интервала (подставляем значения концов интервала в функциональный ряд).
При x = 1 получаем ряд: 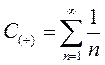
Гармонический ряд, который расходится (показано в предыдущем примере)
Таким образом,
область сходимости исходного ряда С: − 1 < x < 1
Задача № 384. Вычислить определенный интеграл с точностью до 0,001 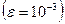 путем предварительного разложения подынтегральной функции в ряд и почленного интегрирования этого ряда
путем предварительного разложения подынтегральной функции в ряд и почленного интегрирования этого ряда
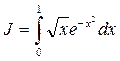
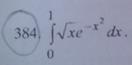
РЕШЕНИЕ:
Используем разложение функции 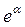 в ряд Маклорена:
в ряд Маклорена:
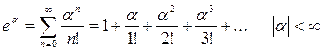
В нашем случае:
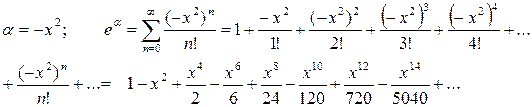
Тогда
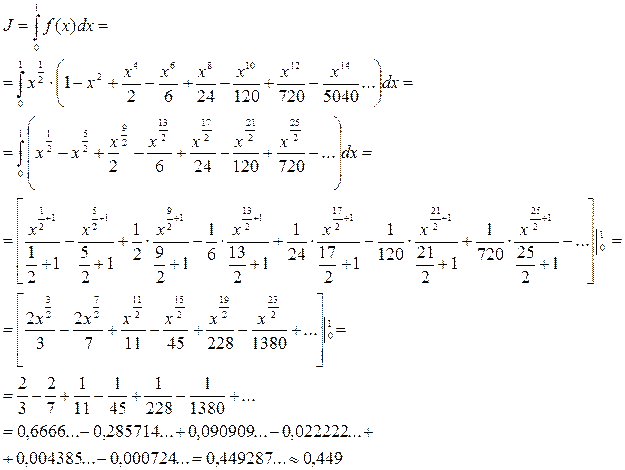
Для обеспечения заданной точности ε=0,001 достаточно взять два первых члена ряда. Третий член по абсолютной величине < ε, и начиная с этого члена и далее, ряд можно отбросить. Этот расчет основан на свойстве знакочередующегося ряда: при замене ряда частичной суммой происходит ошибка, не превышающая по абсолютной величине значения первого из отброшенных членов. Если при вычислениях степенной ряд окажется знакопостоянным, то обеспечение заданной точности вычислений нужно производить по оценке остаточного члена в форме Лагранжа: 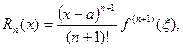 который позволит выбрать необходимое число членов ряда.
который позволит выбрать необходимое число членов ряда.
Таким образом, получаем:
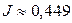
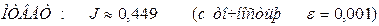
Задача № 404. При указанных начальных условиях найти три первых, отличных от нуля, члена разложения в степенной ряд функции 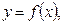 являющейся решением заданного дифференциального уравнения
являющейся решением заданного дифференциального уравнения
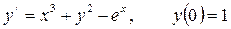
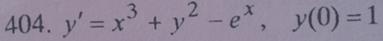
РЕШЕНИЕ:
Решение ДУ находится в виде ряда Тейлора (Маклорена):
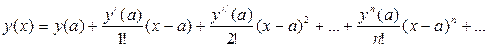
где точка x = a определяется из начальных условий (в данном случае, а = 1).
Значения функции и ее производных для ряда Тейлора находятся из начальных условий непосредственно для первых членов и для остальных членов путем последовательного дифференцирования исходного ДУ, разрешенного относительно старшей производной и вычисленной в точке x = a. Для тех значений x, для которых получившийся ряд сходится, он представляет решение ДУ:
y (a) = y (0) = 1; y / (a) = y / (0) = 03 +12 – e0 = 0 + 1 −1 = 0;
y // (x) = 3 ∙ x + 2 ∙ y ∙ y / − ex; y // (0) = 3 ∙ 0 + 2 ∙ 1 ∙ 0 – e0 = 0 + 0 − 1= −1;
y ///(x) = 2 + 2 ∙ y / ∙ y/ + 2 ∙ y ∙ y // − ex ;
y ///(0) = 2 + 2 ∙ 0 ∙ 0 + 2 ∙ 1 ∙ (−1) − e0 = 2 + 0 − 2 − 1 = − 1;
y(IV) (x) = 2 + 2 ∙ 2 ∙ y / ∙ y// + 2 ∙ y/ ∙ y// + 2 ∙ y ∙ y/// − ex = 2 + 6 ∙ y / ∙ y// + 2 ∙ y ∙ y/// − ex
y(V) (x) = 6 ∙ (y//)2 + 6 ∙ y/ ∙y /// + 2 ∙ y/ ∙ y/// + 2 ∙ y ∙ y(IV) − ex =
= 6 ∙ (y//)2 + 8 ∙ y/ ∙y /// + 2 ∙ y ∙ y(IV) − ex
В данном случае трудно установить закономерность, позволяющую записать выражение в общем виде для n-го члена ряда. Если такая закономерность выявляется, то можно определить радиус сходимости заданного ряда: 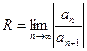 и если получаем
и если получаем 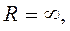 то значит полученное решение ДУ будет справедливо для всех х.
то значит полученное решение ДУ будет справедливо для всех х.
В данном случае решение записывается виде:
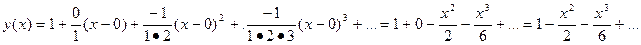 :
:
ОТВЕТ: 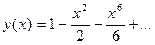
Задача № 424. В ящике имеется 12 деталей, из которых 5 деталей нестандартны. Сборщик наудачу извлекает из ящика 4 детали. Какова вероятность того, что все они будут нестандартны?

РЕШЕНИЕ:
Всего имеем 12 деталей. Число n всевозможных исходов (т.е. способов, которыми можно выбрать 4 детали из 12 равно числу сочетаний
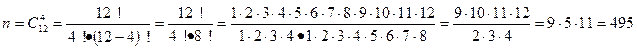
Число m возможных сочетаний, что все детали нестандартные:
Нестандартные (4 из 5):
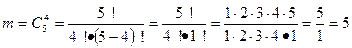
Тогда искомая вероятность определяется как отношение числа благоприятных исходов к числу всех возможных исходов, т.е.:
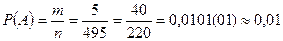
ОТВЕТ:
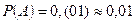
Задача № 444. В некотором водоеме карпы составляют 80%. Найти вероятность того, что из 5 выловленных в этом водоеме рыб окажется: а) 4 карпа; б) не менее 4 карпов.

РЕШЕНИЕ:
Используем формулу Бернулли: вероятность того, что в 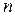 независимых испытаниях, в каждом из которых вероятность появления события равна
независимых испытаниях, в каждом из которых вероятность появления события равна 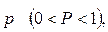 событие наступит
событие наступит 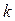 раз (безразлично, в какой последовательности), равна
раз (безразлично, в какой последовательности), равна
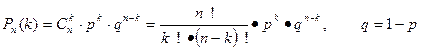
По условию: 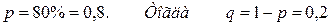
а) 4 карпа:
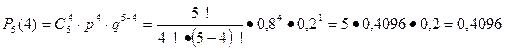
б) не менее 4 карпов:
Не менее 4-x карпов означает, что из 5-ти выловленных в этом водоеме рыб: 4 или 5 карпов.
Последовательно находим:
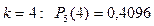
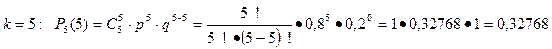
И по теореме сложения вероятностей искомая вероятность равна
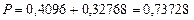
ОТВЕТ:
Задача № 464
Найти: 1) Математическое ожидание 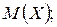 2) Дисперсию
2) Дисперсию 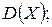
3) Среднее квадратическое отклонение 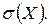
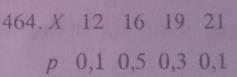
РЕШЕНИЕ:
Дан закон распределения случайной величины Х:
| Х | 12 | 16 | 19 | 21 |
| р | 0,1 | 0,5 | 0,3 | 0,1 |
● Проверка выполнения условия нормировки:
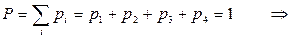
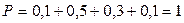
♣ Математическое ожидание:
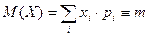
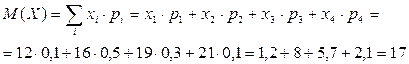
♣ Дисперсия:
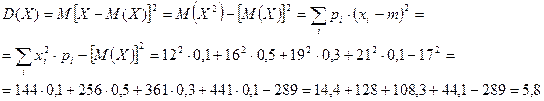
♣ Среднее квадратическое отклонение:
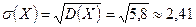
Задача № 484. Случайная величина Х задана функцией распределения вероятностей F(X). Найти: а) вероятность попадания случайной величины Х в интервал 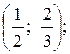 б) плотность распределения вероятностей случайной величины Х; в) математическое ожидание
б) плотность распределения вероятностей случайной величины Х; в) математическое ожидание 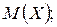 г) дисперсию
г) дисперсию 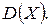

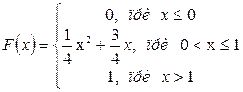
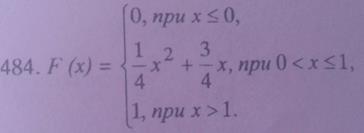
РЕШЕНИЕ:
Найдем плотность распределения:
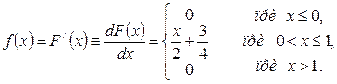
Найдем математическое ожида ние:
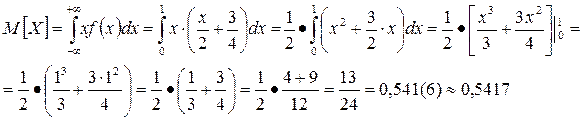
Найдем дисперсию и среднее квадратическое отклонение:
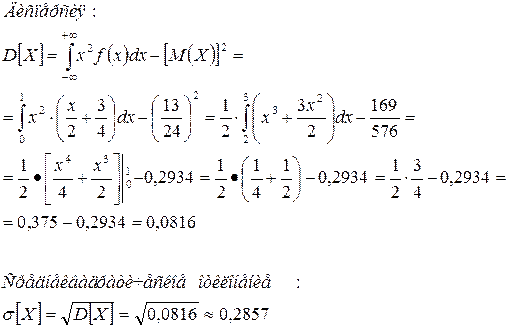
Используя формулу
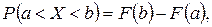
Найдем вероятность попадания Х в заданные интервалы:
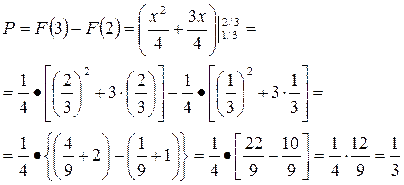
Задача № 504


РЕШЕНИЕ:
1) Если случайная величина Х задана дифференциальной функцией f(x), то вероятность того, что Х примет значение, принадлежащее интервалу 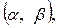 вычисляется по формуле:
вычисляется по формуле:
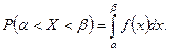
Если величина Х распределена по нормальному закону, то
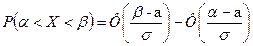 (*)
(*)
где 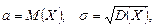
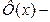 функция Лапласа.
функция Лапласа.
Функция Лапласа табулирована (значения даны в справочной таблице) и имеет следующие свойства:
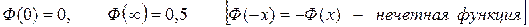
Находим:
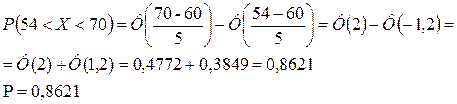
2) Если Х − длина детали, то по условию задачи эта величина должна быть в интервале 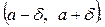 Подставив в формулу (*)
Подставив в формулу (*) 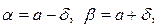 получим:
получим:
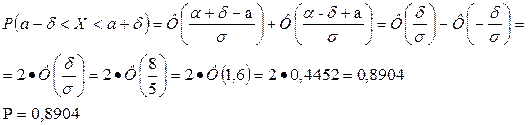
 2020-08-05
2020-08-05 217
217








