2020-08-05
151
Числовой последовательностью называется бесконечное число занумерованных чисел 
или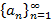 
. Задать последовательность можно формулой для 
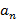, например, 
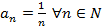и на числовой оси (рисунок 30).
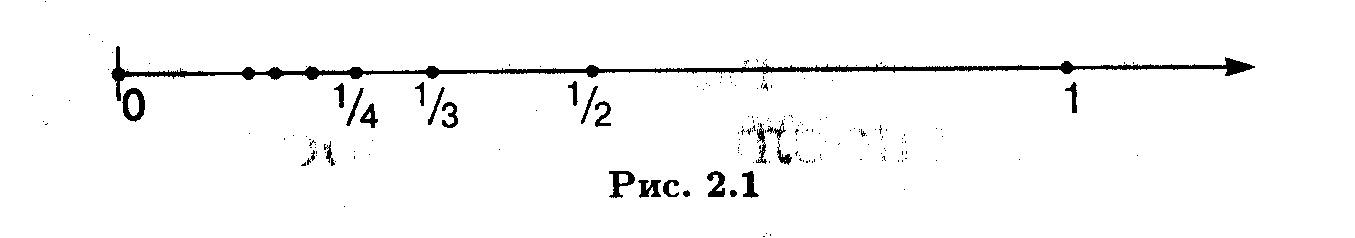
Рисунок 30. Отображение чисел на числовой прямой.
Помимо вышеуказанных способов, числа можно задать на координатной плоскости, рассмотрев график функции натуральной переменой 
.
Последовательность 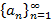называется ограниченной, если можно указать 
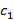и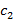 
, такие что 
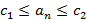для всех элементов последовательности
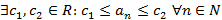
Геометрически ограниченность последовательности означает, что все элементы находятся на отрезке 
(на рисунке 30 последовательность ограничена отрезком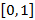 
). В случае рассмотрения последовательности на координатной плоскости, тогда все точки графика находятся внутри полосы, ограниченно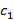й и .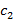
Последовательность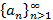 
называется монотонной, если выполняется одно из условий:
1. 
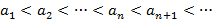(строго возрастает);
2. 
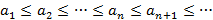(не убывает);
3. 
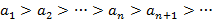(строго убывает);
4. 
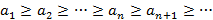(не возрастает).
Число A называется пределом последовательности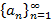 
, если для любой 
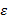– окрестности точки A (даже для сколь угодно малой) можно указать номер N, который зависит от 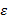, начиная с которого все члены последовательности будут находится внутри этой окрестности
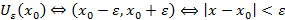
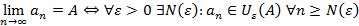
У последовательности не может быть более одного предела.
Свойства конечных пределов:
1. 
;
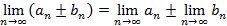2. 
;
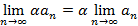3. 
;
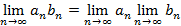4. 
;
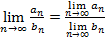5. Если 
, тогда 
.
