2020-08-05
1356
Последовательность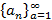 
называют бесконечно малой последовательностью (БМП), если ее предел равен нулю.
Последовательность 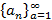имеет предел равный положительной или отрицательной бесконечности, если для любого числа m найдется номер N, зависящей от m, такой что начиная с этого номера все члены последовательности больше или меньше m
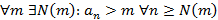
Если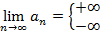 
, тогда последовательность называется бесконечно большой последовательностью (ББП).
Если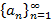 
- БМП, а 
- ББП, тогда 
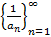- ББП и 
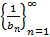- БМП соответственно. Символически предельная теорема записывается так: 
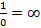и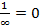 
. У последовательности может не быть предела, например 
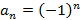или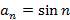 
. Если последовательность монотонна и ограничена, тогда у нее существует предел.
Рассмотрим выражение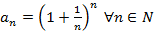 
, в котором для первых пяти членов последовательности выполняется монотонное возрастание и все элементы принадлежат отрезку 
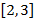. Предел данной последовательности называется вторым замечательным пределом и имеет вид
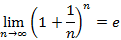
Понятие функции
Функция – отношение между элементами, при котором изменение в одном элементе влечет за собой изменение в другом. В нашем случае функция – соответствие между элементами двух множеств, установленное по такому правилу, что каждому элементу первого множества соответствует один и только один элемент второго множества.
Исходя из рассматриваемого определения функция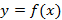 
представляет собой тройку объектов X, f и Y, где
1. Множество X – область задания или область определения функции;
2. Множество Y – область значений функции;
3. F – правило, по которому каждому элементу 
сопоставляется некоторый элемент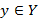 
.
Обозначенной буквой x – аргумент функции; y – частное значение функции.
Числовой функцией одной переменной 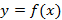с областью определения 
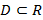называется правило, которое каждому 
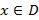ставит в соответствие однозначно определенное 
.
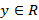График функции 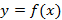с областью определения D – множество всех точек вида 
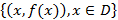. Рассмотрим графики элементарных функций:
1. Функция прямой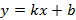 
. График функции прямой относительно коэффициентов k и b представлен на рисунке 31.
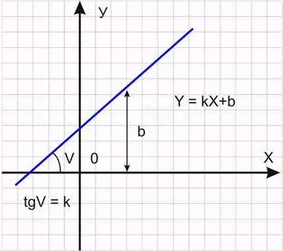
Рисунок 31. График прямой.
2. Квадратичная функция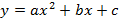 
. Графиком данной функции является парабола, которая представлена на рисунке 32.
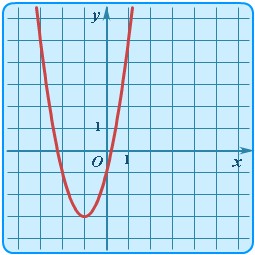
Рисунок 32. График квадратичной функции.
3. Степенная функция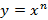 
. Пример степенной функции 
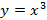представлен на рисунке 33.
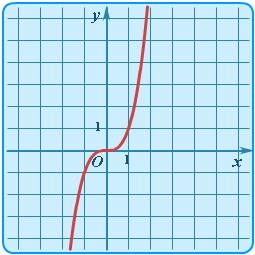
Рисунок 33. Степенная функция .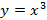
Пример степенной функции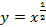 
представлен на рисунке 34.
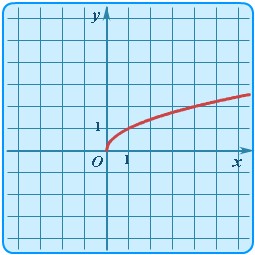
Рисунок 34. Функция квадратного корня.
Пример степенной функции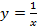 
представлен на рисунке 35.
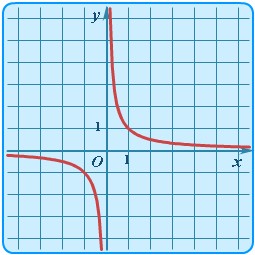
Рисунок 35. Функция обратной пропорциональности.
4. Показательная функция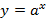 
. График показательной функции представлен на рисунке 36.
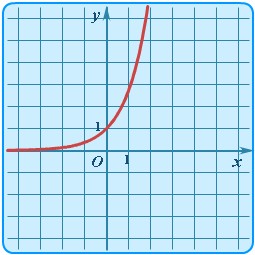
Рисунок 36. График показательной функции.
5. Логарифмическая функция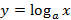 
. График логарифмической функции представлен на рисунке 37.
Рисунок 37. График логарифмической функции.
6. Функции синуса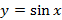 
, косинуса 
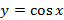, тангенса 
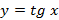и котангенса
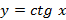. Графики соответствующих функций представлены на рисунке 38.
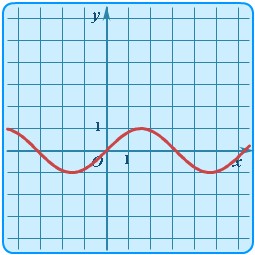
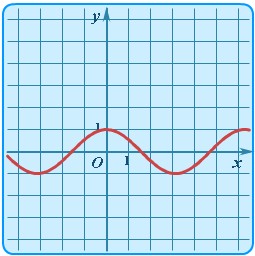
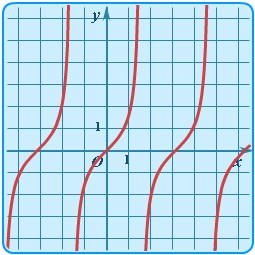
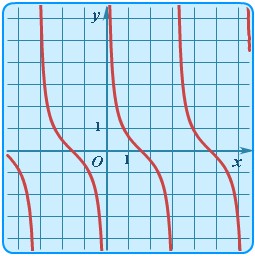
Рисунок 38. Графики тригонометрических функций, распложенные в порядке перечисления.
Обратная функция – функция, обращающая зависимость, вырезаемую данной функцией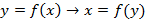 
. Пример расположения взаимно обратных функции представлены на рисунке 39.
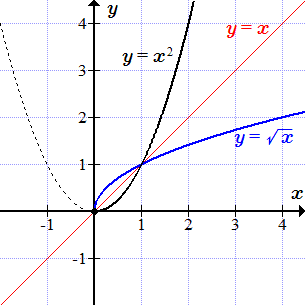
Рисунок 39. Взаимно обратные функции.
Свойства функций:
1. Монотонность. Функция называется монотонной, если она относится к следующим видам: возрастающая, убывающая, неубывающая или невозрастающая.
2. Периодичность. Функция имеет период t, если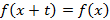 
для всех x из области определения.
3. Ограниченность. Функция называется ограниченной на области определения или на некотором промежутке, если ее значения ограничены некоторыми константами для всех x из области определения: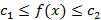 
.
4. Четность и нечетность. Функция называется четной, если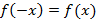 
для вей области определения. Функция называется нечетной, если 
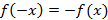для всей области определения.
Пусть заданы две функци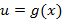и 
и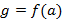 
, тогда функция 
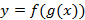называется композицией функции f и g.
