Сущность этого метода заключается в том, что по отношению к выделенной ветви ab с сопротивлением 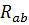 вся остальная часть сложной цепи, содержащая источники ЭДС, может быть заменена одним эквивалентным генератором с ЭДС
вся остальная часть сложной цепи, содержащая источники ЭДС, может быть заменена одним эквивалентным генератором с ЭДС 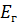 и внутренним сопротивлением
и внутренним сопротивлением 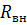 .
.
Таким образом, для определения тока 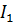 в интересующей нас ветви необходимо найти напряжение
в интересующей нас ветви необходимо найти напряжение 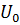 при разрыве ветви ab и сопротивление
при разрыве ветви ab и сопротивление 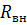 всей прочей части цепи при замкнутых накоротко содержащихся в ней источниках ЭДС. [5]
всей прочей части цепи при замкнутых накоротко содержащихся в ней источниках ЭДС. [5]
1. Найдем 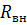 , рассматривая исходную схему как активный двухполюсник относительно зажимов a и b. Для нахождения сопротивления убираем ветвь cb с источником тока и закорачиваем источники ЭДС:
, рассматривая исходную схему как активный двухполюсник относительно зажимов a и b. Для нахождения сопротивления убираем ветвь cb с источником тока и закорачиваем источники ЭДС:
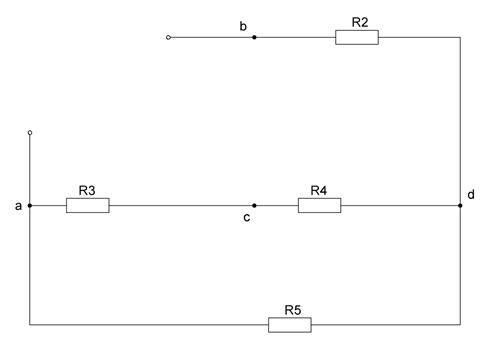
Рисунок 15 – Схема для нахождения 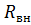
Тогда 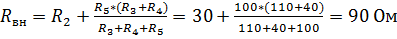 .
.
2. Найдем напряжение 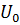 на зажимах генератора, для чего убираем из схемы резистор с сопротивлением
на зажимах генератора, для чего убираем из схемы резистор с сопротивлением 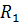 .
.
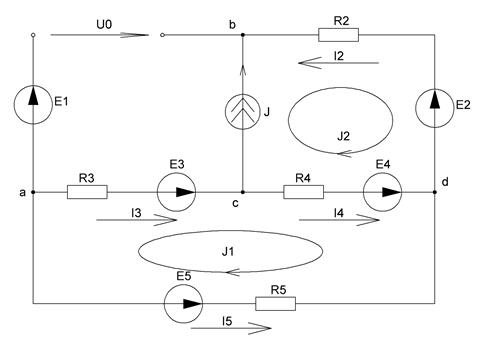
Рисунок 16 – Схема для нахождения 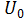
Найдем токи 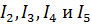 методом контурных токов. Для этого выберем два контура: bdcb с контурным током
методом контурных токов. Для этого выберем два контура: bdcb с контурным током 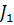 и acda с контурным током
и acda с контурным током 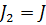 . Так как значение тока во втором контуре известно, составим уравнение для нахождения контурного тока
. Так как значение тока во втором контуре известно, составим уравнение для нахождения контурного тока 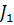 :
:
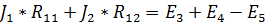 , где
, где
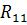 – собственное сопротивление контура bdcb, равное сумме сопротивлений, входящих в этот контур:
– собственное сопротивление контура bdcb, равное сумме сопротивлений, входящих в этот контур: 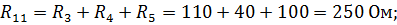
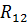 – сопротивление смежной ветви контуров bdcb и acda, равное
– сопротивление смежной ветви контуров bdcb и acda, равное 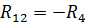 .
.
Тогда значение тока 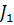 можно найти из следующего выражения:
можно найти из следующего выражения:
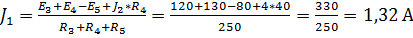 .
.
Действительные токи равны соответственно: 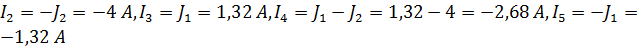 .
.
Напряжение 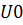 найдем из контура bdcab при обходе его по часовой стрелке. По второму закону Кирхгофа для этого контура имеем:
найдем из контура bdcab при обходе его по часовой стрелке. По второму закону Кирхгофа для этого контура имеем: 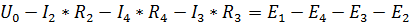 .
.
Откуда 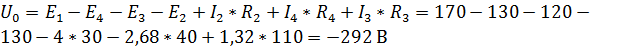 .
.
Тогда сила тока в ветви ab будет равна: 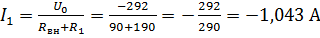 .
.
 2020-08-05
2020-08-05 322
322








