Тема 1. Методы начисления процентов в финансовых расчетах

Министерство сельского хозяйства Российской Федерации

ФГОУ ВПО "Красноярский государственный аграрный университет"

 

 

ОСНОВЫ ФИНАНСОВОЙ

 МАТЕМАТИКИ

Методические указания для проведения практических занятий

по дисциплинам "Деньги, кредит, банки" и

 "Базисные финансовые расчеты"

 

 

Красноярск 2009

     Составитель: Е.И. Коваленко

 

Основы финансовой математики: Метод. указания для проведения практических занятий / Краснояр. гос. аграр. ун-т. – Красноярск, 2009. - 32 с.

 

 

Методическое указание содержит последовательное и систематизированное изложение проверенных практикой методов количественного анализа финансовых и кредитных операций. Подробно изложены различные методы начисления процентов, обобщающие характеристики потоков платежей, методики определения эффективности краткосрочных и долгосрочных финансовых операций. По каждой рассматриваемой теме приведены условия задач.

Методические указания предназначены студентов обучающихся по специальностям:

- 080105.65 "Финансы и кредит";

- 080109.65 "Бухгалтерский учет, анализ и аудит";

- 080504.65 "Государственное и муниципальное управление".

 

Рецензент: к.э.н., доцент Власова Е.Ю.

 

Печатается по решению редакционно-издательского совета

Красноярского государственного аграрного университета

 

Ó ФГОУ ВПО "Красноярский государственный аграрный университет", 2009

СОДЕРЖАНИЕ

ВВЕДЕНИЕ....................................................................................................... 4

Тема 1. Методы начисления процентов в финансовых расчетах……..4

Тема 2. Декурсивный и антисипативный метод
начисления процентов...................................................................... 8

Тема 3. Определение календарной базы начисления простых процентов 10

Тема 4. Начисление процентов на депозитах до востребования.......... 11

Тема 5. Начисление процентов при изменении процентной ставки
в течение срока................................................................................ 13

Тема 6. Начисление сложных процентов................................................... 14

Тема 7. Начисление процентов при регулярных взносах....................... 16

Тема 8. Депозитные и сберегательные сертификаты коммерческих банков 18

Тема 9. Дисконтирование и банковский учёт............................................ 22

Тема 10. Начисление банковских процентов в условиях инфляции... 24

Тема 11. Погашение кредита единовременным платежом..................... 26

Тема 12. Погашение кредита частями........................................................ 27

БИБЛИОГРАФИЧЕСКИЙ СПИСОК......................................................... 31

 

ВВЕДЕНИЕ

В современной России очевидна потребность в овладении методикой финансовых расчетов. В связи с этим в рамках различных дисциплин изучаются отдельные темы и проблемы, которые можно отнести к высшим финансовым вычислениям. Настоящее методическое указание содержит последовательную характеристику современных методов финансовых вычислений и позволяет ознакомиться с основными направлениями количественного финансового анализа, с применяемым при этом математическим аппаратом, понять важность и необходимость аналитического решения соответствующих проблем.

Финансовая математика – это система практически необходимых расчетов доходности финансовых, инвестиционных и торговых операций во времени с учетом инфляции, валютных курсов, процента и прочих юридических и практических условий выполнения договоров. Финансовая математика вводит начинающего экономиста в мир количественного анализа финансовых операций. Она охватывает довольно узкий круг методов, когда возникает необходимость в условиях сделки оговорить три момента:

- стоимостные характеристики: цены, размеры платежей и долговые обязательства;

- временные характеристики: сроки платежей, даты и продолжительности периодов, различные отсрочки и т.д.;

- процентные ставки, заданные как в явной, так и в неявной форме.

Финансовая математика изучает сами схемы платежей и правила начисления процентов, а также дает объективный ответ на естественный вопрос: "Какая из возможных финансовых сделок выгоднее?". Не многие из экономических дисциплин могут похвастаться подобной конкретностью.

 

Тема 1. Методы начисления процентов в финансовых расчетах

"Процент есть цена, которую люди платят за то, чтобы получить ресурсы сейчас, вместо того, чтобы ждать до тех пор, пока они заработают деньги, на которые эти ресурсы можно купить " Пол Хейне.

Проценты (процентные деньги) – это сумма доходов от предоставления денег в долг в различных формах (открытие депозитных счетов, выдача кредитов, покупка облигаций или сберегательных сертификатов, реализация товаров в кредит, учет векселей др.). Сумма начисленных процентов зависит от суммы долга, срока его выплаты и процентной ставки. Процесс увеличения суммы денег во времени в связи с присоединением процентов называют наращением, или ростом, этой суммы. Процентные деньги могут выплачиваться по мере их начисления или присоединяться к сумме долга.

В зависимости от способа начисления, проценты делятся на простые и сложные.

Простые проценты – это метод начисления, при котором сумма процентов определяется в течение всего периода, исходя из первоначальной величины долга, независимо от количества периодов начисления и их длительности.

Простые проценты начисляются по формуле:

Б = С (1 + 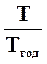 ´ К),                                (1)

где: Б – конечная сумма, полученная вкладчиком (кредитором) по истечению периода Т;

С – первоначальная (исходная) сумма вклада (долга);

Т – период, в течение которого происходило начисление (в днях);

Т_год – количество дней в году. Принимается равным 360 или 365 (в зависимости от метода определения Т);

К – норма доходности (ставка процентов по вкладам).

Сложные проценты – метод расчета процентов, при котором начисления происходят на первоначальную сумму вклада (долга) и на прирост вклада (долга), т.е. сумму процентов, начисленных после первого периода начисления. Таким образом, база для начисления сложных процентов (в отличие от простых) будет увеличиваться с каждым периодом начисления.

Суть сложных процентов в том, что происходит начисление процента на процент.

Формула сложных процентов имеет следующий вид:

Б = С (1+ К)^Т,                                        (2)

где: Т – период начисления в годах.

Кроме основных двух методов начисления банковских процентов существует также третий.

Если срок хранения вклада больше года и не является целым числом лет, то проценты могут начисляться по смешанной ставке.

Б = С (1 + К)^{T l} ´ (1 + DТК),                            (3)

где: T l – целое число лет в течение срока вклада;

DТ – остаток периода в годах.

Т = T l + DТ

Начисление смешанных процентов даёт более точный результат, в то время как при сложных процентах итог приближённый.

 

Задание

1. Требуется обеспечить получение 100 000 руб. через полгода. Сколько надо вложить для этой цели денег в коммерческий банк при начислении простых и сложных процентов в размере 15% годовых. Сделать вывод, какой метод более выгоден клиенту.

2. Депозит в размере 150 000 руб. открыт в банке на 2 года под 20% годовых. Найти сумму начисленных процентов с использованием простой и сложной ставок. Сделать вывод, какой метод более выгоден вкладчику.

3. Вкладчик размещает 85 000 руб. в банке на 1,5 года, проценты начисляются по сложной ставке, которая составляет 21% годовых. Рассчитать сумму начисленных процентов (приближённое и точное значение).

4. Банк предлагает разместить вкладчику 700 000 руб. на срочный депозит в трех вариантах: а) на 1 день под 6 % годовых с последующим реинвестированием ежедневно в течение месяца; б) на 10 дней под 10 % годовых с последующим реинвестированием каждую декаду в течение месяца; в) на 1 месяц под 18 % годовых. Определить наиболее выгодный вариант вложения денежных средств.

5. Найти, в течение какого количества лет вклад в размере 1 500 руб. возрастет до 3 000 руб. при начислении процентов по простой ставке, 13% годовых.

6. Вкладчик собирается положить в банк сумму 15 000 руб. с целью накопления 16 500 руб. Ставка процентов будет составлять 21% годовых. Найти срок в днях, за который вкладчик сможет накопить требуемую сумму. Необходимо учесть, что банк использует при расчетах фактическое значение количества дней в году.

7. Клиент, решивший внести на депозит 20 000 руб., хочет накопить через год не менее 27000 руб. Необходимо найти требуемую простую ставку процентов, на основании которой он может выбрать банк для размещения своих средств.

8. Имеются две суммы денег, одна больше другой на 5000 руб.

- бóльшая сумма вложена на 6 месяцев при ставке 5% годовых.

- мéньшая сумма внесена на 3 месяца при ставке 6% годовых.

- процентный доход за бόльшую сумму вдвое больше процентного дохода за мéньшую сумму. Необходимо найти величину этих денежных капиталов.

9. На какой временной период должен быть вложен капитал при 12% годовых, чтобы процентный доход был равен тройной сумме капитала?

10. Денежная сумма, величиной 10000 руб., внесена в банк на 4 месяца под 10% годовых. Определить величину процентного дохода вкладчика.

11. Банк ежегодно начисляет сложные проценты на вклады по ставке 13% годовых. Определить сумму, которую надо положить в банк, чтобы через 3 года накопить 1 млн. руб.

12. Определить простую ставку процентов, при которой первоначальный капитал в размере 20 000 руб., достигнет через 90 дней 30 000 руб.

13. Определить период начисления, за который первоначальный капитал в размере 20 000 руб. вырастет до 60 000 руб., если банк проводит расчеты с клиентами по простой ставке 120 % годовых.

14. Банк в 200_ году принимал вклады от населения под простые и сложные проценты на 3 месяца под 21 % годовых, на 6 месяцев – под 18,5 % годовых, на 12 месяцев – 20,09 % годовых. Сравнить доходность различных вкладов.