Арифметический квадратный корень

1. Квадратным корнем из числа а называют число, квадрат которого равен а.
2. Арифметическим квадратным корнем из числа а называется неотрицательное число, квадрат которого равен а.
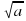3. = b, если выполняются два условия: 1) b ≥ 0; 2) 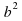= а.
4. При а ‹ 0 выражение 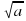не имеет смысла.
5. При любом а, при котором выражение 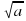имеет смысл, верно равенство ( = а.
6. Выражение 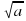имеет смысл при любом а ≥ 0
7. Если а ≥ 0 и b 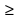0, то 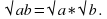Корень из произведения неотрицательных множителей равен произведению корней из этих множителей.
8. Если а ≥ 0 и b 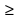0, то 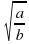= 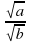. Корень из дроби, числитель которой неотрицателен, а знаменатель положителен, равен корню из числителя, делённому на корень из знаменателя.
9. При любом значении х верно равенство 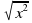= | x |.

Функция у = 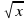и её график.

1. Если х = 0, то у = 0, поэтому начало координат принадлежит графику функции. 0
2. Если х › 0, у › 0: график расположен в первой координатной четверти.
3. Большему значению аргумента соответствует дольше значение функции; график функции идёт вверх.

Квадратное уравнение и его корни.

1. Квадратным уравнением называется уравнение вида a +bx +c = 0, где а,b и с – некоторые числа, причём а ≠ 0.
2. Квадратное уравнение в котором а = 1, называют приведённым квадратным уравнением.
3. Если в квадратном уравнении a +bx +c = 0 хотя бы один из коэффициентов b или с равен нулю, то такое уравнение называют неполным квадратным уравнением
4. При решении квадратного уравнения a +bx +c = 0 целесообразно поступать следующим образом: 1. Вычислить дискриминант и сравнить его с нулём; 2. Если дискриминант положителен, то воспользоваться формулой корней 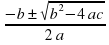, если дискриминантотрицателен, то записать, что корней нет.
5. Сумма корней приведённого квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.(Теорема Виета).
6. Если числа m и n таковы, что их сумма равна - p, а произведение равно g, то эти числа являются корнями уравнения +px +g = 0 (Обратная теореме Виета)