Цель: сформировать определения понятия основного тригонометрического тождества; научиться доказывать тригонометрические тождества
Теоретические сведения к практическому занятию:
Т.к. 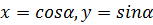 , уравнение единичной окружности имеет вид
, уравнение единичной окружности имеет вид 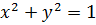 , то
, то 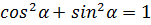 .
.
Это равенство, выполняемое при любых значениях α называется основным тригонометрическим тождеством.
Доказательство:
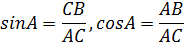
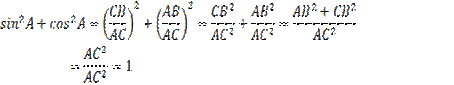
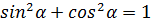
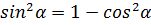
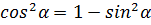
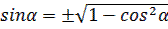
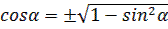
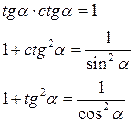
Равенство, справедливое при всех допустимых значениях, входящих в него букв, называют тождеством.
Способы доказательства тождеств:
- преобразование левой части к виду правой;
- преобразование правой части к виду левой;
- установление того, что разность между левой и правой частями равна нулю;
- преобразование левой и правой частей к одному и тому же выражению.
Пример. Вычислить 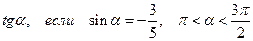
Решение. 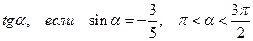
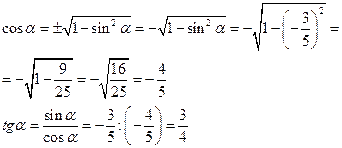
Пример: Найти 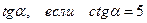
Решение:
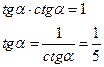
39
Пример. Доказать тождество: 
Доказательство:
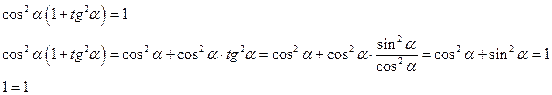
Самостоятельная работа:
1.Вычислить:
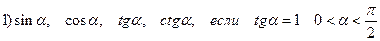
2. Доказать тождества:
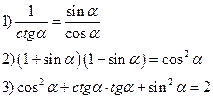
Содержание практического занятия:
А. Ответить на вопросы:
1) Назовите основное тригонометрическое тождество. Приведите примеры.
2) Используя основное тригонометрическое тождество, выразите функции синуса и косинуса.
3) Назовите тригонометрическое тождество для функций тангенса и котангенса.
4) Дайте определение тождества. Приведите примеры.
5) Назовите способы доказательства тождеств.
Б. Выполнить задания:
1.Вычислить:
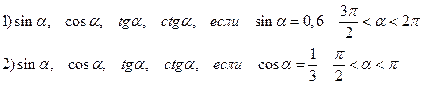
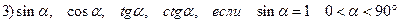
 2020-09-24
2020-09-24 107
107








