Цель: сформировать определения понятий синуса, косинуса и тангенса углов; сформировать умение находить знаки синусов, косинусов и тангенсов в различных четвертях
Теоретические сведения к практическому занятию:
Синусом угла α называется ордината точки, полученной поворотом точки (1;0) вокруг начала координат на угол α.
Косинусом угла α называется абсцисса точки, полученной поворотом точки (1;0) вокруг начала координат на угол α.
Тангенсом угла α называется отношение синуса угла α к его косинусу.
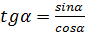
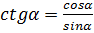

Знаки тригонометрических функций
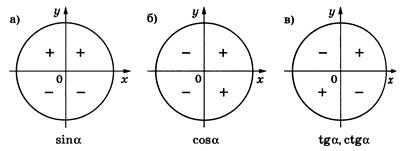
Таблица значений тригонометрических функций
| Градусы α | 0 | 30 | 45 | 60 | 90 | 180 | 270 | 360 |
| Радианы α | 0 | 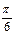
| 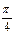
| 
| 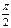
| 
| 
| 
|

| 0 | 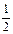
| 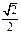
| 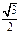
| 1 | 0 | -1 | 0 |

| 1 | 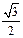
| 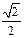
| 
| 0 | -1 | 0 | 1 |
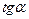
| 0 | 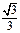
| 1 | 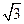
| - | 0 | - | 0 |
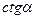
| - | 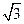
| 1 | 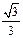
| 0 | - | 0 | - |
Пример. Вычислить 
Решение. 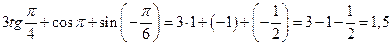
Самостоятельная работа:
1) Приведите определения синуса, косинуса и тангенса, используя прямоугольный треугольник
2) Вычислить:
а) 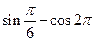 г)
г) 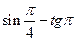
б)  д)
д) 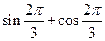
в) 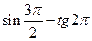 е)
е) 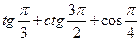
Содержание практического занятия:
А. Ответить на вопросы:
1) Дайте определение синуса данного угла. Укажите знаки функции синуса для координатных четвертей.
2) Дайте определение косинуса данного угла. Укажите знаки функции косинуса для координатных четвертей.
3) Дайте определение тангенса и котангенса данного угла. Укажите знаки функций тангенса и котангенса для координатных четвертей.
4) Приведите таблицу значений тригонометрических функций. Приведите примеры.
Б. Выполнить задания:
Вычислить:
а)  м)
м) 
б) 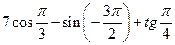 н)
н) 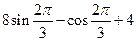
в)  о)
о) 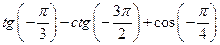
г) 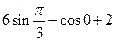 к)
к) 
д) 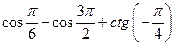 и)
и) 
е) 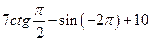 з)
з) 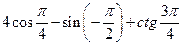
ж) 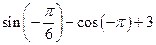 л)
л) 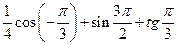
 2020-09-24
2020-09-24 239
239








