2020-09-24
117
Цель: сформировать умение находить пределы последовательностей.
Теоретические сведения к практическому занятию:
Пусть существует последовательность действительных чисел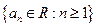 
.
Число а называется пределом последовательности
4
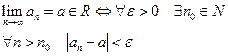
Пример 1. Вычислить предел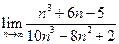 
Решение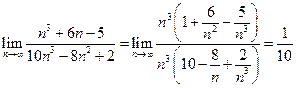 
Пример 2. Вычислить предел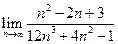 
Решение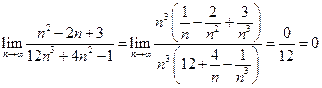 
Пример 3. Вычислить предел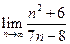 
Решение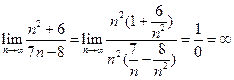 
Пример 4. Вычислить предел 
Решение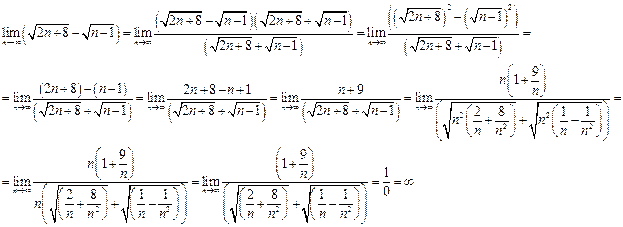 
Самостоятельная работа:
1) Выполните доклад на тему «История возникновения и развития пределов»
2) Вычислить пределы последовательностей:
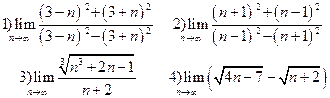
Содержание практического занятия
А. Ответить на вопросы:
1) Дайте определение предела последовательности. Приведите примеры.
2) Приведите пример последовательности, предел которой равен нулю.
3) Приведите пример последовательности, предел которой равен бесконечности.
Б. Выполнить задания:
Задание 1. Вычислить пределы последовательностей:
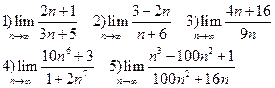
Задание 2. Вычислить пределы последовательностей:
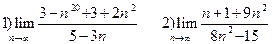
Тема: Предел функции
Цель: сформировать умение находить пределы функций.
|
|
|
Теоретические сведения к практическому занятию:
Число А называют пределом функции f (x) при 
(и пишут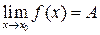 
), если для любого 
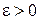найдется число 
зависящее от, такое, что для всех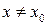 
, удовлетворяющих условию 
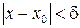, выполняется неравенство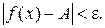 
Теоремы о пределах:
1. 
(c =const).
2. Если 
то:
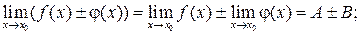
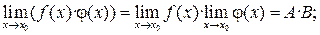
Чтобы найти предел элементарной функции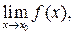 
нужно предельное значение аргумента подставить в функцию и посчитать. При этом, если х = х 0 принадлежит области определения функции, то значение предела будет найдено, оно равно значению функции в точке х = х 0. При вычислении пределов полезно использовать следующие соотношения. Если 
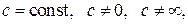то, учитывая свойства б.б. и б.м. функций, получим:
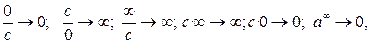если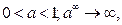 
если a >1.
Случаи, в которых подстановка предельного значения аргумента
в функцию не дает значения предела, называют неопределенностями;
к ним относятся неопределенности видов:
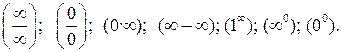
Пример 1. Вычислить предел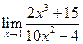 
Решение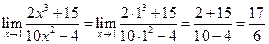 
Пример 2. Вычислить предел 
Решение 
Пример 3. Вычислить предел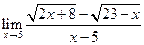 
Решение 
Самостоятельная работа:
Задание 1. Вычислить пределы функций:
