Площадь трапеции равна произведению длины средней линии трапеции на высоту

Теорема Пифагора: В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Теорема, обратная теореме Пифагора: Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то треугольник прямоугольный.

Прямоугольные треугольники, у которых длины сторон выражаются целыми числами, называются пифагоровыми треугольниками.

Треугольник со сторонами 3, 4, 5 часто называют египетским.

Отношением отрезков АВ и CD называется отношение их длин, т. е.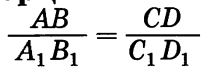

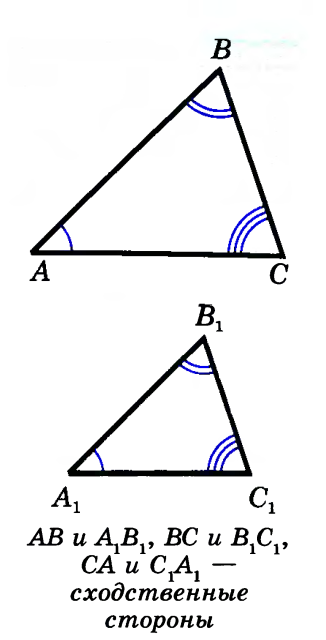Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого.

Другими словами, два треугольника подобны, если для них можно ввести обозначения ABC и А₁В₁С₁ так, что:

 

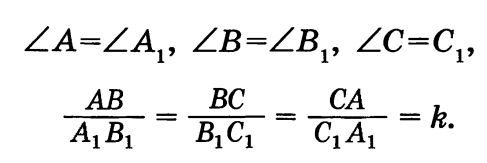
Число k, равное отношению сходственных сторон подобных 

треугольников, называется коэффициентом подобия.

Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.

Признаки подобия треугольников:

1. Если два угла одного треугольника соответственно равны двум углам другого, то такие

треугольники подобны.

2. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны.

3. Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.

Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.

Теорема: Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.

Медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2:1, считая от вершины.

Высота прямоугольного треугольника, проведенная из вершины прямого угла, разделяет треугольник на два подобных прямоугольных треугольника, каждый из которых подобен данному треугольнику.

Отрезок XY называется средним пропорциональным (или средним геометрическим) для отрезков АВ и CD, если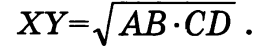

Свойства:

1°. Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное  для отрезков, на которые делится гипотенуза этой высотой.

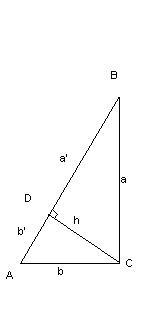2°. Катет прямоугольного треугольника есть среднее пропорциональное  для гипотенузы и отрезка гипотенузы, заключенного между катетом и высотой, проведенной из вершины прямого угла.

 

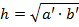
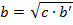
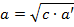
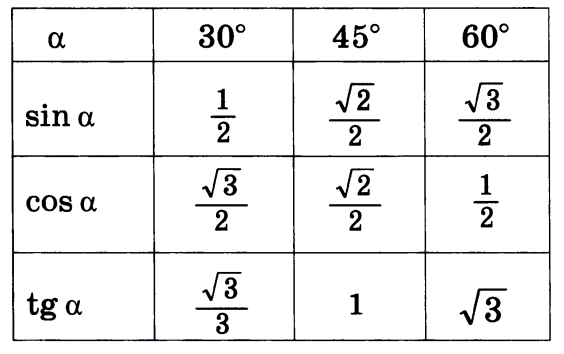
Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.

Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.

Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему катету.

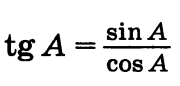 т. е. тангенс угла равен отношению синуса к косинусу этого угла.

Если острый угол одного прямоугольного треугольника равен острому углу другого прямоугольного треугольника, то синусы этих углов равны, косинусы этих углов равны и тангенсы этих углов равны.

Основное тригонометрическое тождество:

Взаимное расположение прямой и окружности в зависимости от соотношения между d и r. Возможны три случая:

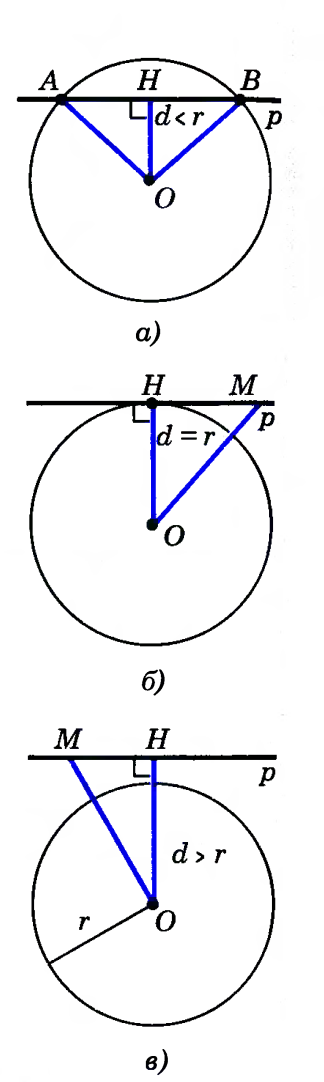
1. Если расстояние от центра окружности до прямой меньше радиуса окружности (d < r), то прямая и окружность имеют две общие точки. В этом случае прямая называется секущей по отношению к окружности.

2. Если расстояние от центра окружности до прямой равно радиусу окружности, то прямая и окружность имеют только одну общую точку.

3. Если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность не имеют общих точек.

Прямая, имеющая с окружностью только одну общую точку, называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности.

Свойства касательной к окружности:

1. Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.

2. Отрезки касательных к окружности, проведенные из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.

Обратная теорема (признак касательной):

Если прямая проходит через конец радиуса, лежащий на окружности, и перпендикулярна к этому радиусу, то она является касательной.

Дуга называется полуокружностью, если отрезок, соединяющий ее концы, является диаметром окружности.

· Если дуга АВ окружности с центром в точке О меньше полуокружности или является полуокружностью, то ее градусная мера считается равной градусной мере центрального угла АОВ

· Если же дуга АВ больше полуокружности, то ее градусная мера считается равной (360° — угол АОВ).

Угол с вершиной в центре окружности называется ее центральным углом.

Сумма градусных мер двух дуг окружности с общими концами равна 360°.

Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным углом.

Если дуга расположена внутри вписанного угла, то говорят, что вписанный угол опирается на эту дугу.

Теорема: Вписанный угол измеряется половиной дуги, на которую он опирается.