Теория по геометрии 8 класс

Сумма длин всех сторон называется периметром многоугольника.

Многоугольник с n вершинами называется n -угольником; он имеет n сторон.

Две вершины многоугольника, принадлежащие одной стороне, называются соседними.

Отрезок, соединяющий любые две несоседние вершины, называется диагональю многоугольника.

Любой многоугольник разделяет плоскость на две части, одна из которых называется внутренней, а другая — внешней областью многоугольника.

Многоугольник называется выпуклым, если он лежит по одну сторону от каждой прямой, проходящей через две его соседние вершины.

Cумма углов выпуклого n-уголника равна (п—2) 180°.

Две несмежные стороны четырехугольника называются противоположными. Две вершины, не

являющиеся соседними, также называются противоположными.

Cумма углов выпуклого четырехугольника равна 360°.

Параллелограммом называется четырехугольник, у которого противоположные стороны попарно параллельны.

Свойства параллелограмма:

1°. В параллелограмме противоположные стороны равны и противоположные углы равны.

2°. Диагонали параллелограмма точкой пересечения делятся пополам.

Признаки параллелограмма:

1°. Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник— параллелограмм.

2°. Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник — параллелограмм.

3°. Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник — параллелограмм.

Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны.

Параллельные стороны трапеции называются ее основаниями, а две другие стороны — боковыми сторонами.

Трапеция называется равнобедренной, если ее боковые стороны равны.

Трапеция, один из углов которой прямой, называется прямоугольной.

Теорема Фалеса: если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки.

Прямоугольником называется параллелограмм, у которого все углы прямые.

Так как прямоугольник является параллелограммом, то он обладает всеми свойствами параллелограмма: в прямоугольнике противоположные стороны равны, а диагонали точкой пересечения делятся пополам.

Свойство прямоугольника: Диагонали прямоугольника равны.

Признак прямоугольника: Если в параллелограмме диагонали равны, то этот параллелограмм — прямоугольник.

Ромбом называется параллелограмм, у которого все стороны равны.

Свойство ромба: Диагонали ромба взаимно перпендикулярны и делят его углы пополам.

Квадратом называется прямоугольник, у которого все стороны равны.

Прямоугольник является параллелограммом, поэтому и квадрат является параллелограммом, у которого все стороны равны, т. е. ромбом. Отсюда следует, что квадрат обладает всеми свойствами прямоугольника и ромба:

1. Все углы квадрата прямые.

2. Диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам и делят углы квадрата пополам.

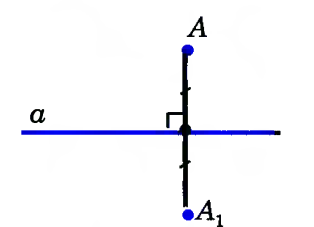
Две точки А и А₁ называются симметричными относительно прямой а, если эта прямая проходит через середину отрезка АА₁ и перпендикулярна к нему. Каждая точка прямой а считается симметричной самой себе.

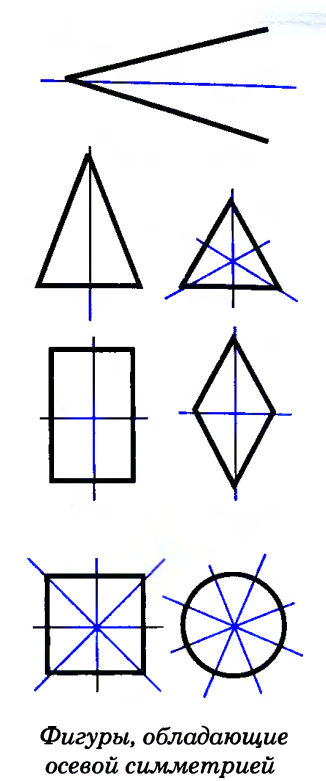
Фигура называется симметричной относительно прямой а, если для каждой точки фигуры симметричная ей точка относительно прямой а также принадлежит этой фигуре. Прямая а называется осью симметрии фигуры. Говорят также, что фигура обладает осевой симметрией.

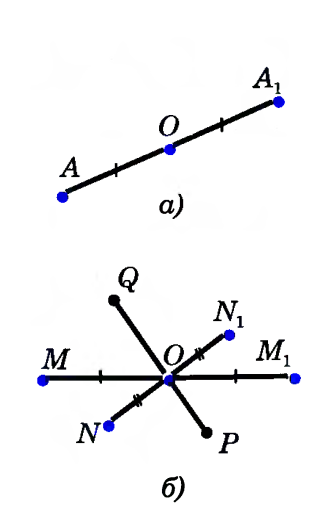
Две точки А и А₁называются симметричными относительно точки О, если О— середина отрезка АА₁. Точка О считается симметричной самой себе.

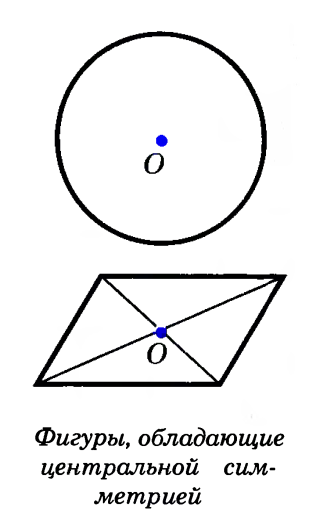
Фигура называется симметричной относительно точки О, если для каждой точки фигуры симметричная ей точка относительно точки О также принадлежит этой фигуре.

Точка О называется центром симметрии фигуры. Говорят также, что фигура обладает центральной симметрией.

Так, если за единицу измерения отрезков принят сантиметр, то за единицу измерения площадей принимают квадрат со стороной 1 см. Такой квадрат называется квадратным сантиметром и обозначается см². Аналогично определяется квадратный метр (м²), квадратный миллиметр (мм²) и т. д.