Решить систему линейных уравнений  методом простой итерации
методом простой итерации
1) Приведем исходную систему к виду с преобладающими диагональными коэффициентами и введем в Mathcad матрицы коэффициентов при неизвестных в левой части и свободных членов:
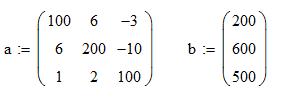
2) Получаем преобразованную систему, для чего разделим каждое уравнение на свой диагональный коэффициент и выразим из каждого уравнения диагональное неизвестное.

3) Проверим условия сходимости итерационного процесса, «погружая» систему в пространство с одной из трех метрик ρ1, ρ2, ρ3. Используем для этого встроенные функции Mathcad:

Все коэффициенты меньше единицы, значит, систему можно погрузить в пространство с любой из метрик. Пусть это будет пространство с метрикой ρ2.
Итак, итерационный процесс сходится, причем α = 0,08.
4) Находим критерий достижения заданной точности. Для достижения точности  приближения нужно находить до тех пор, пока будет выполняться неравенство
приближения нужно находить до тех пор, пока будет выполняться неравенство 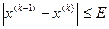 , т.е. расстояние между двумя соседними приближениями не должно превышать числа Е.
, т.е. расстояние между двумя соседними приближениями не должно превышать числа Е.
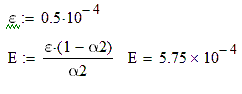
5) Вычисляем значение итерационной последовательности:
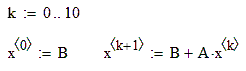

6) Для определения, какое приближение будет являться решением, необходимо найти расстояния между двумя соседними приближениями по метрике ρ2.
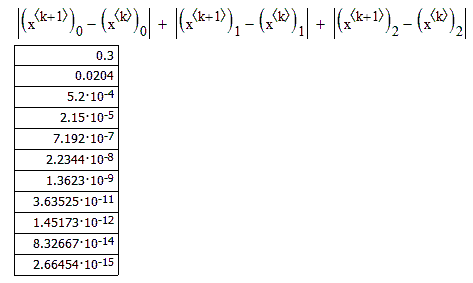
Полученное четвертое значение суммы модулей разностей коэффициентов при неизвестных, равное 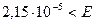 , удовлетворяет условию критерия. Это значит, что в таблице значений х третий столбец является решением системы уравнений.
, удовлетворяет условию критерия. Это значит, что в таблице значений х третий столбец является решением системы уравнений.
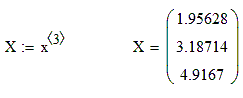
 2020-09-24
2020-09-24 198
198








