Рассчитайте вектор состояния системы на 3-м шаге

6 7 8 9 10 11 12

Вероятности состояния системы могут определяться с помощью рекуррентной формулы, представляющей матричное уравнение

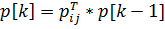
где p[k] – вектор состояния системы после k шагов;

p^T_ij - транспонированная матрица переходов;

p[k-1] – вектор состояния системы после k-1 шагов.

Создадим программу расчета матричного уравнения:

% Подготовка массива

pk=zeros(2,1);

% Вектор состояния на первом шаге

pk1=[0.8;0.2];

% Матрица переходов

pij=[0.8 0.2; 0.9 0.1];

% Цикл от 2 до 500 шага

for k=2:500

% Расчет матричного уравнения

pk=pij'.*pk1;

% Если разница между последним и предпоследним

% состояниям меньше 0.0001, то расчет останавливается

if abs(pk(1,1)-pk1(1,1))<0.0001

disp(['Шаг №' num2str(k) ' достигнута точность 0.001'])

break

end

pk1 = pk;

end

disp('Матрица состояний')

disp(pk)

Когда величина вероятности предпоследнего и последнего состояний меньше 0.0001, считаем что Марковский процесс перешел в стационарную стадию. Это подтверждает основное свойства Марковских цепей – через счетное количество шагов (период приработки) вероятность перехода из одного состояние в другое становится неизменной. В теории Марковских процессов распределение вероятности для установившегося режима называют инвариантным.

Рассмотрим систему с 4-мя дискретными состояниями (рис. 7):

0 - Работа

1 - Простой

2 - Ремонт

3 - Утилизация

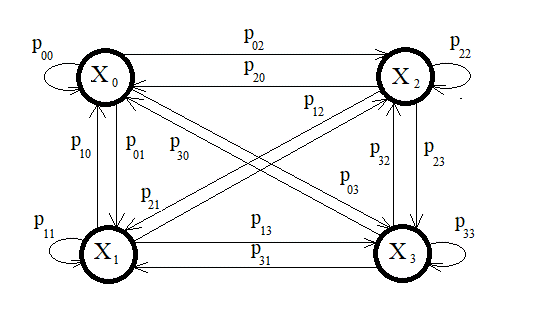
Рис. 7

Матрица переходов системы из i – го состояния в j – ое составляет

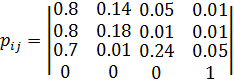
Проанализируйте вероятности переходов. В данном случае имеет место состояние, из которого нет выхода – Утилизация. Скорее всего, именно в этом состоянии и закончится Марковский процесс, и как такового установившегося режима не будет.

Составим программу, которая покажет количество шагов до тех пор, когда изменение вероятностей состояний практически не меняется.

% Подготовка массива для k – го шага

pk=zeros(4,1);

%В начальный момент времени

p0=[1 0 0 0];

%Матрица переходов

pij=[0.8 0.14 0.05 0.01; 0.8 0.18 0.01 0.01; 0.7 0.01 0.24 0.05; 0 0 0 1];

% Вектор состояния на первом шаге

pk1=[0.8; 0.15; 0.05; 0];

% Цикл от 2 до 500 шага

for k=2:500

% Расчет матричного уравнения