2020-09-24
89
1) Область определения функции.
2) Чётность, нечётность.
3) Периодичность.
4) Точки пересечения с осями.
5) Точки разрыва, вертикальные асимптоты.
6) Интервалы монотонности, точки экстремума.
7) Точки перегиба, интервалы выпуклости и вогнутости.
8) Наклонные, горизонтальные асимптоты.
Пример: Исследуйте функцию 
и постройте её график.
Решение.
1) 
2) 
- функция нечётная, график симметричен относительно начала координат;
3) функция непериодическая;
4) точка пересечения с осями Ox и Oy - 
;
5) найдём односторонние пределы для точек разрыва:
; 
;
; 
.
- точка разрыва второго рода;
- точка разрыва второго рода.
Прямые , - вертикальные асимптоты.
6) найдём первую производную функции 
:
;
из уравнения 
получаем критические точки 
, 
, 
.
Определяем знаки первой производной.
В результате получаем две точки экстремума 
и 
. Находим значения функции в этих точках: 
, 
.
7) найдём вторую производную функции 
:
;
при 
получаем точку 
.
|
|
|
Определяем знаки второй производной.
Точка является точкой перегиба. На интервалах 
и 
график функции вогнутый, а на интервалах 
и 
– выпуклый.
8) найдём коэффициенты k и b:
; 
.
Уравнение наклонной асимптоты имеет вид 
.
РАЗДЕЛ 3. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Тема 10. ОПРЕДЕЛЕНИЕ И СВОЙСТВА НЕОПРЕДЕЛЕННОГО ИНТЕГРАЛА
Первообразная функции.
Определение 1. Пусть на некотором промежутке X задана функция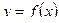 
. Функция 
, определённая на X, называется первообразной для 
на этом промежутке, если для всех 
верно равенство 
.
Под промежутком X будем понимать отрезок, интервал, полуинтервал: 
, 
, 
, 
, 
, 
, 
, 
.
Примеры:
1) 
, 
2) 
, 
3) 
, 
4) 
, 
У всякой функции существует бесконечно много первообразных. Следующая теорема позволяет свести нахождение всех первообразных данной функции к отысканию одной из них.
Теорема. Если 
и 
– две первообразные от функции 
на промежутке X, то
.
Геометрическая иллюстрация первообразной
Графики всех первообразных получаются из графика одной первообразной параллельным переносом вдоль оси ординат.
