Рассмотрим на плоскости кривую, которая является графиком дифференцируемой функции  .
.
Определение 1. Кривая обращена выпуклостью вверх на интервале  , если все точки кривой лежат ниже любой её касательной на этом интервале.
, если все точки кривой лежат ниже любой её касательной на этом интервале.
Кривая обращена выпуклостью вниз на интервале  , если все точки кривой лежат выше любой её касательной на этом интервале.
, если все точки кривой лежат выше любой её касательной на этом интервале.
Кривую, обращенную выпуклостью вверх, будем называть выпуклой, а обращённую выпуклостью вниз – вогнутой.

Теорема 1. Если во всех точках интервала  вторая производная функции
вторая производная функции 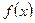 отрицательна, т.е.
отрицательна, т.е.  , то кривая
, то кривая 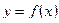 обращена выпуклостью вверх (кривая выпукла).
обращена выпуклостью вверх (кривая выпукла).
Теорема 2. Если во всех точках интервала  вторая производная функции
вторая производная функции  положительна, т.е.
положительна, т.е.  , то кривая
, то кривая 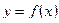 обращена выпуклостью вниз (кривая вогнута).
обращена выпуклостью вниз (кривая вогнута).
Определение 2. Точка, отделяющая выпуклую часть непрерывной кривой от вогнутой, называется точкой перегиба кривой.
В точке перегиба касательная пересекает кривую, так как с одной стороны от этой точки кривая лежит под касательной, а с другой стороны – над нею.
Теорема 3 (необходимое условие точки перегиба). Для того чтобы график функции 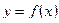 имел перегиб в точке
имел перегиб в точке 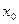 , необходимо, чтобы функция была дифференцируема в точке
, необходимо, чтобы функция была дифференцируема в точке 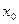 , и чтобы в этой точке вторая производная либо не существовала, либо была равна нулю.
, и чтобы в этой точке вторая производная либо не существовала, либо была равна нулю.
Теорема 4 (достаточное условие точки перегиба). Пусть кривая определяется уравнением  . Если
. Если  или
или  не существует и при переходе через точку
не существует и при переходе через точку  производная
производная  меняет знак, то точка кривой с абсциссой
меняет знак, то точка кривой с абсциссой  есть точка перегиба.
есть точка перегиба.
Пример: Найдите точки экстремума и точки перегиба функции  .
.
Решение. Находим область определения функции:  .
.
Первая производная функции равна:
 .
.
Приравняем производную к нулю и найдем критические точки:  . При переходе через точку
. При переходе через точку  производная меняет знак с «-» на «+», значит, в этой точке функция имеет минимум. При переходе через точку
производная меняет знак с «-» на «+», значит, в этой точке функция имеет минимум. При переходе через точку  производная не меняет знака, следовательно, в этой точке функция не имеет экстремума.
производная не меняет знака, следовательно, в этой точке функция не имеет экстремума.
Найдём значение функции в точке минимума  .
.
Вторая производная функции равна:
 .
.
Приравняем вторую производную к нулю и найдем точки:  . При переходе через эти точки производная меняет знак, следовательно, они являются точками перегиба.
. При переходе через эти точки производная меняет знак, следовательно, они являются точками перегиба.
Найдём значения функции в точках перегиба:  ,
,  .
.
Результаты исследования сведены в таблицу:
| x | 
| 
| 
| 
| 
|
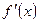
| - | 0 | + | 0 | + |

| убывает | 
| Возрастает | 
| Возрастает |
| x | 
| 
| 
| 
| 
|

| + | 0 | - | 0 | + |
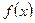
| вогнутость | 
| выпуклость | 
| Вогнутость |
Асимптоты.
Определение. Прямая A называется асимптотой кривой, если расстояние  от переменной точки M кривой до этой прямой при удалении точки M в бесконечность стремится к нулю.
от переменной точки M кривой до этой прямой при удалении точки M в бесконечность стремится к нулю.

Различаются вертикальные (параллельные оси ординат) и наклонные асимптоты.
1) Вертикальные асимптоты.
Если  ,
,  или
или  , то прямая
, то прямая  есть асимптота кривой
есть асимптота кривой  .
.
Пример: Найдите вертикальные асимптоты кривой  .
.
Решение. Найдём область определения функции  :
:

Найдём односторонние пределы:
 ;
;  ;
;
 ;
;  .
.
Прямые  ,
,  являются вертикальными асимптотами.
являются вертикальными асимптотами.

2) Наклонные асимптоты.
Пусть кривая 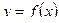 имеет наклонную асимптоту
имеет наклонную асимптоту  . Тогда
. Тогда  ,
,  .
.
Пример: Найдите асимптоты кривой  .
.
Решение. 1) Найдём односторонние пределы:
 ;
;  .
.
 - вертикальная асимптота.
- вертикальная асимптота.
2) Найдём коэффициенты k и b:
 ;
;  .
.
Получаем уравнение наклонной асимптоты  .
.
 2020-09-24
2020-09-24 154
154








