Основные свойства определённого интеграла

1. Постоянный множитель можно выносить за знак определённого интеграла, т.е., если 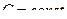, то

.

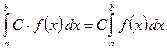2. Определённый интеграл от алгебраической суммы нескольких функций равен алгебраической сумме интегралов от слагаемых.

Так, в случае двух слагаемых

.

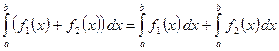3. Если на отрезке , где 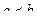, функци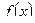и  и 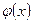 удовлетворяют условию 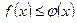, то

.

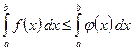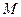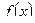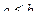4. Если  и  – наименьшее и наибольшее значения функции  на отрезке  и , то

.

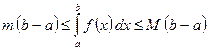Если 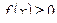, то это свойство иллюстрируется геометрически следующим образом:

Площадь криволинейной трапеции 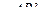 содержится между площадями прямоугольников  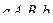и .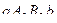

5. Теорема о среднем. Если функция 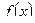 непрерывна на отрезке 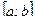, то на этом отрезке найдётся такая точка 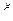, что справедливо следующее равенство:

.

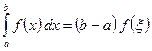6. Для любых трёх чисел a, b и c справедливо равенство

,

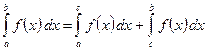если только все эти три интеграла существуют.

Геометрическая иллюстрация.

Есл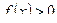и  и 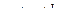, то площадь трапеции  равна сумме площадей трапеци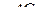й  и .

Тема 14. ВЫЧИСЛЕНИЕ ОПРЕДЕЛЁННОГО ИНТЕГРАЛА. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ