Определение определённого интеграла

На каждом из отрезков 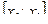, , 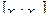,  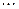возьмём по точке, которые обозначим , , , , 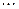где , , , .

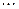В каждой из этих точек вычислим значения функции , , , .

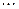Составим сумму:

           (1)

Эта сумма называется интегральной суммой для функции  на отрезке .

Так как при произвольном , принадлежащем отрезку , будет  и все , то . Следовательно,

,

т.е.

.                                                 (2)

Сумма  зависит от выбора точек  внутри отрезков , а также от способа разбиения отрезка  на отрезки .

Обозначим через  наибольшую из длин отрезков . Если , то .

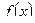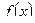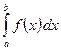Если при любых разбиениях отрезка , таких, что  и при любом выборе точек  сумма  стремится к одному и тому же пределу J, то говорят, что функция  интегрируема на отрезке , функцию  называют подынтегральной функцией, а предел J называют определённым интегралом от функции  на отрезке . Его обозначают  и пишут:

.

Число a называется нижним пределом интегрирования, а число b – верхним пределом интегрирования. Отрезок  называется отрезком интегрирования, переменная x – переменной интегрирования.

Замечание. Если функция  непрерывна на отрезке , то она интегрируема на этом отрезке. Среди разрывных функций есть как интегрируемые, так и неинтегрируемые.

Геометрический смысл определённого интеграла.

Если 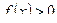, то интеграл  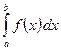численно равен площади криволинейной трапеции, ограниченной кривой , прямыми ,  и осью Ox:

.

Замечания. 1) Определённый интеграл зависит только от вида функции 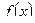 и пределов интегрирования, но не зависит от переменной интегрирования, которую можно обозначить любой буквой:

.

2)

3)