Способы изображения синусоидальных величин

 

Под переменной ЭДС понимается ЭДС, изменяющаяся по синусоидальному закону (рис. 3.2).

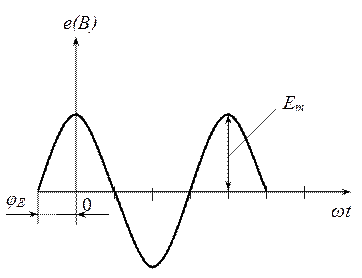
Рис. 3.2

 

Закон изменения синусоидальной ЭДС записывается в следующем виде:

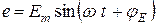(В),                           (3.2)

где e – мгновенное значение ЭДС (В), это значение ЭДС в каждой точке синусоиды;

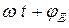 – фаза синусоидальных колебаний;

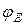 – это начальная фаза для ;

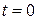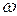 – угловая частота синусоидальных колебаний (1/с).

Частотой f называется число периодов в секунду:

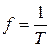             (Гц),

где T – период, это время одного цикла колебаний (с).

Угловая частота 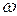 и частота f связаны соотношением:

.

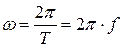Для источника переменного напряжения закон изменения записывается в следующем виде:

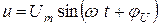(В)                            (3.3)

Для синусоидального тока закон изменения записывается аналогичным образом:

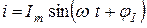            (А)                  (3.4)

При сравнении выражений (3.2), (3.3), (3.4) видно, что форма записи одинакова, разница лишь в угле начальной фазы .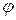

Частота переменного тока f = 50 Гц в Европе и 60 Гц в США и Японии.

Для того, чтобы сравнить характеристики цепей постоянного и переменного токов, вводится понятие действующего значения синусоидальной величины:

тока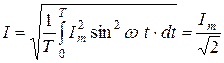

напряжения ;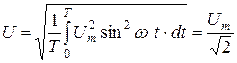

ЭДС .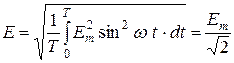

Электроприборы в цепях переменного тока измеряют действующее значение тока, напряжения, ЭДС и мощности.

Тригонометрическая форма записи синусоидальных величин неудобна при расчёте электрических цепей переменного тока, поэтому в электротехнике синусоидальные функции изображают в виде комплексных чисел, согласно следующему положению.

Любая синусоидальная функция может быть изображена в виде вектора на комплексной плоскости, величина которого равняется синусоидальной функции, а угол, образованный с осью действительных чисел, равняется углу начальной фазы синусоидального колебания.

Комплексная плоскость – это плоскость, образованная с осью действительных чисел (+ 1) и осью мнимых чисел (+ j), где .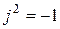

На рис. 3.3 показано изображение амплитуды тока 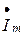на комплексной плоскости

 

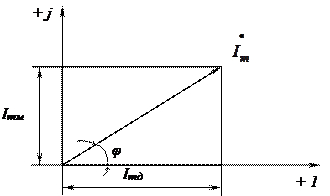Рис. 3.3

 

Из рис. 3.3 следует, что 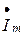 – комплекс  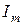(точка показывает комплексную величину);  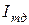– проекция комплекса на ось действительных чисел;  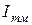– проекция комплекса на ось мнимых чисел;  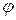– угол начальной фазы.

Существуют следующие способы изображения комплексных чисел:

алгебраическое

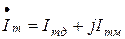;                                            (3.5)

тригонометрическое

;                                (3.6)

где , .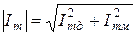

показательное

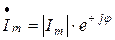;                                              (3.7)

где e – основание натуральных логарифмов.

Аналогично изображаются и комплексы напряжений 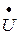 и ЭДС .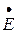

Рассмотрим пример, когда требуется определить сумму двух токов 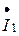 и , и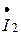зображённых на комплексной плоскости (рис. 3.4).

 

 

 

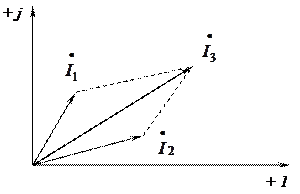Рис. 3.4

 

Взаимное расположение векторов на комплексной плоскости называется векторной диаграммой. Для определения суммы двух токов 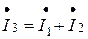 достаточно сложить их по правилу параллелограмма.

Применение комплексных чисел при расчёте электрических цепей переменного тока позволяет перейти от дифференциальных и интегральных уравнений к алгебраическим.