Конденсатор в цепи переменного тока

 

Пусть в цепь переменного напряжения 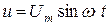 включен конденсатор (рис. 3.11).

Тогда ток, проходящий через конденсатор будет равен [1]:

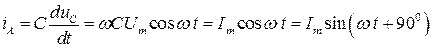,             (3.19)

где .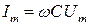

Введём понятие ёмкостного сопротивления X_C

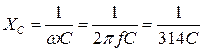, (Ом)                (3.20)

где f = 50 Гц, емкость С измеряется в фарадах (Ф).

 

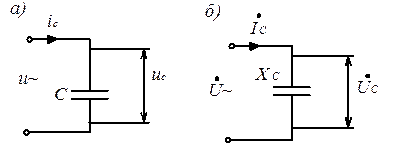
Рис. 3.11

 

Графики изменения напряжения на конденсаторе 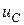 и тока  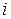показаны на рис. 3.12.

 

Рис. 3.12

 

Построим векторную диаграмму для цепи, содержащей конденсатор. Построение начинаем с комплексной плоскости (рис. 3.13). Параллельно оси действительных чисел (+ 1) строим вектор действующего напряжения на конденсаторе 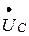. Теперь, сравнивая (рис. 3.12) законы изменения напряжения на конденсаторе  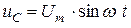и тока  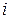через конденсатор  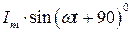делаем вывод, что вектор тока I опережает вектор падения напряжения  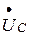на конденсаторе на угол .

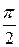Закон Ома в комплексном виде для конденсатора запишется так:

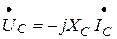,                                    (3.21)

где 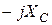 – комплекс емкостного сопротивления;

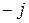 показывает, что падение напряжения на конденсаторе  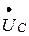отстает от тока  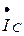на угол .

 

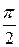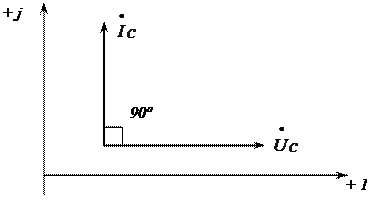Рис. 3.13

 

Этой форме записи закона Ома в комплексном виде соответствует схема замещения, показанная на рис. 3.11, б.

Мгновенная мощность на конденсаторе равна

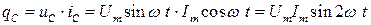       (3.22)

Мощность в цепи, содержащей емкостный элемент, называют реактивной емкостной мощностью Q_C и измеряют в вольт-амперах реактивных (вар).

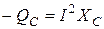  (вар)                        (3.23)

Знак «минус» у мощности Q_C говорит о том, что в первую и третью четверть колебаний конденсатор отдаёт мощность источнику в отличие от индуктивности, которая в первую и третью четверть потребляет от источника реактивную мощность + Q_L.

 

Последовательное соединение резистора, индуктивности