И ёмкости в цепи переменного тока

Последовательным соединением элементов называется такое соединение, когда по всем элементам идёт один и тот же ток, а приложенное напряжение равняется геометрической сумме падений напряжений на этих элементах согласно второму закону Кирхгофа.

Схема последовательного соединения R, x_L, и x_C приведена на рис. 3.14, а.

Рис. 3.14

Второй закон Кирхгофа в комплексном виде запишется следующим образом:

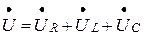(3.24)

С учетом вышеприведённых выражений

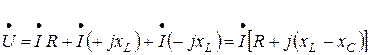(3.25)

Выражение в квадратных скобках обозначим через Z и назовем его полным комплексным сопротивлением цепи.

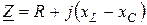(Ом) (3.26)

По величине 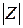равняется

(Ом)

Тогда закон Ома для последовательно соединенных элементов в комплексной форме запишется в виде

(3.27)

Этой форме записи закона Ома будет соответствовать схема замещения, показанная на рисунке 3.14, б. Схемы «а» и «б» называются эквивалентными.

Величина тока 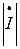при последовательном соединении элементов будет

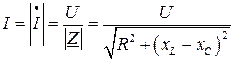(А)

Построим векторную диаграмму для последовательного соединения резистора, индуктивности и емкости.

Построение начинаем с комплексной плоскости (рис. 3.15, а), параллельно оси действительных чисел строим вектор действующего значения тока 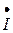, так как ток является общим для всех элементов. Далее по вектору тока 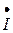строим вектор падения напряжения на резисторе 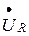(совпадающий с током по направлению). Из конца вектора 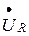строим вектор падения напряжения на индуктивности 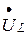под углом 90⁰ к вектору тока 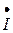в сторону опережения. Из конца вектора 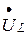строим вектор падения напряжения на конденсаторе 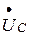( 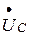отстает от вектора тока на угол 90⁰) и получаем точку «а». Соединив точку «а» с началом вектора 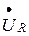, получаем вектор полного приложенного напряжения , при этом образуется треугольник напряжений. Угол 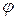между векторами тока 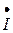и вектором полного напряжения называется углом сдвига фаз, и он характеризует режим работы электрической цепи. Векторная диаграмма позволяет качественно контролировать аналитические расчёты электрических цепей.

Если все стороны треугольника напряжений разделить на ток 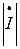, то получим подобный треугольнику напряжений треугольник сопротивлений (рис. 3.15, б).

Если все стороны треугольника сопротивлений умножить на , то получим треугольник мощности (рис. 3.15, в).

Рис. 3.15

Из треугольника мощности следует, что S – полная мощность электрической цепи, равна:

(В·А) (3.28)

Реактивная мощность цепи

(вар) (3.29)

Активная мощность цепи

(Вт) (3.30)

Для характеристики режима работы электрической цепи в электротехнике вводится понятие , который показывает степень использования полной мощности источника S:

(3.31)

Проанализируем режимы работы электрической цепи:

1. 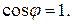В этом случае S = P, Q = 0 и полное сопротивление Z = R. Цепь потребляет только активную мощность P.

2. 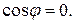В этом случае S = Q, P = 0 и полное сопротивление цепи Z = X, цепь обладает только реактивными свойствами.

3. В этом случае и полное сопротивление 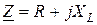, цепь обладает активно-индуктивными свойствами, и она потребляет активную P и реактивную Q_L мощности.

4. 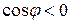. В этом случае , и полное сопротивление 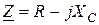, цепь обладает активно-ёмкостными свойствами, она потребляет из сети активную мощность P, но отдает в сеть реактивную – Q_С.